Μαθηματικά Β' Λυκείου (Τράπεζα Θεμάτων)

70 / 130

69
Τράπεζα Θεμάτων Μαθηματικά Κατεύθυνσης Β’ – Εκδόσεις ΜΠΑΧΑΡΑΚΗ
Απάντηση:
α. Ο συντελεστής διεύθυνσης της ΑΒ είναι ΑΒ
5 2
λ 3
1 0

 

και η εξίσωσή της:
  y 2 3 x 0 3x y 2 0      
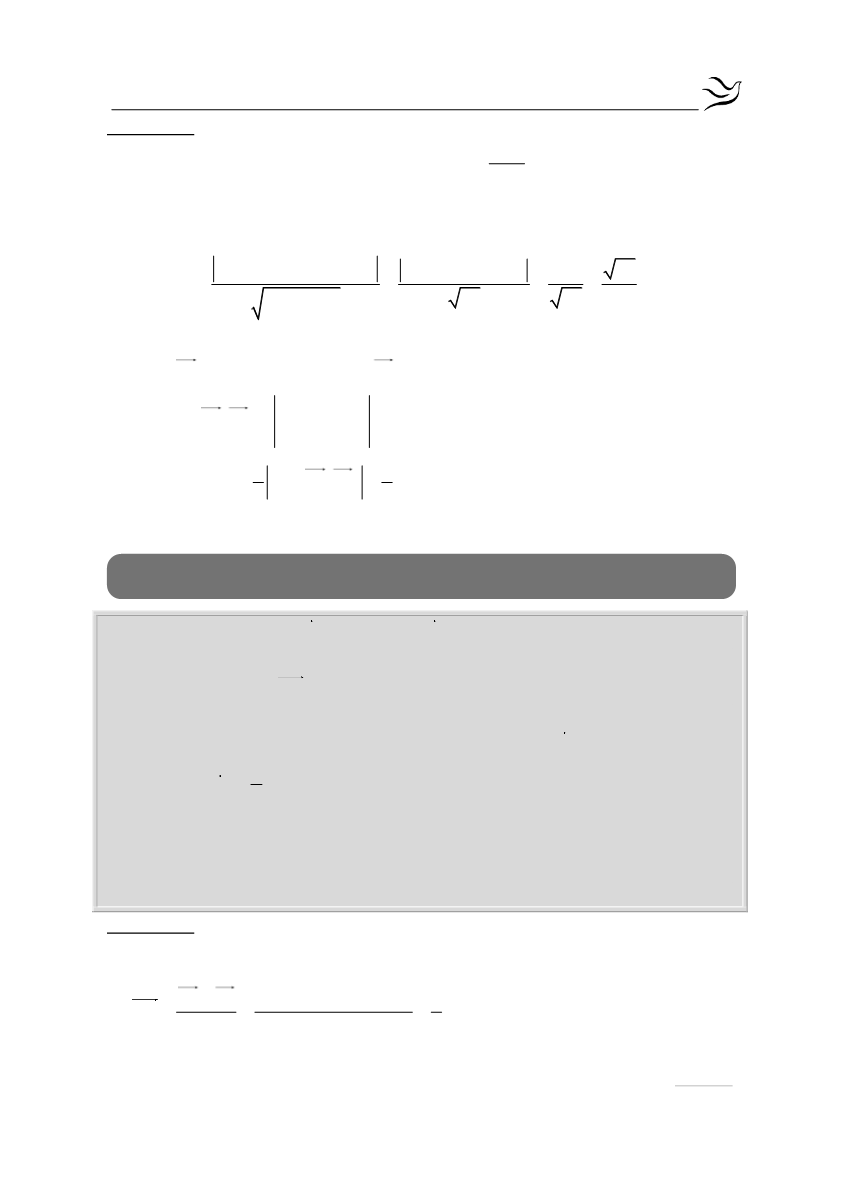
β. Η απόσταση είναι :
 
   
 2
2
3 t 1 3t 2 2 3t 3 3t 2 2 1 10
d Γ,ΑΒ
10 10 10
3 1
        
   
 
δηλαδή ανεξάρτητο του t.
Είναι         AB 1 0,5 2 1,3 , ΑΓ t 1,3t 2 2 t 1,3t 4          
και   1 3
det ΑΒ,ΑΓ 3t 4 3t 3 1.
t 1 3t 4
      
 
Οπότε     1 1
ΑΒΓ det ΑΒ,ΑΓ
2 2
  , δηλαδή ανεξάρτητο του t.
Σε τρίγωνο ΑΒΓ είναι     ΑΒ λ,λ 1 ,     ΑΓ 3λ,λ 1 , όπου  λ 0 και   λ 2 ,
και Μ είναι το μέσο της πλευράς ΒΓ
α. Να αποδείξετε ότι  
 ΑΜ 2λ,λ .
(Μονάδες 7)
β. Να βρείτε την τιμή του λ για την οποία το διάνυσμα ΑΜ είναι κάθετο στο
διάνυσμα  
  
 
2
α , λ
λ
.
(Μονάδες 8)
γ. Για την τιμή του λ που βρήκατε στο ερώτημα β), να υπολογίσετε το εμβαδόν
του τριγώνου ΑΒΓ.
(Μονάδες 10)
Απάντηση:
α. Από τον τύπο της διανυσματικής ακτίνας μέσου τμήματος, αν θεωρήσουμε
το Α ως σημείο αναφοράς, έχουμε :
   
   
λ, λ 1 3λ, λ 1 ΑΒ ΑΓ 1
ΑΜ 4λ,2λ 2λ, λ .
2 2 2
   
   
ΘΕΜΑ 4 - 18609