Μαθηματικά Β' Λυκείου (Τράπεζα Θεμάτων)

Εκδόσεις ΜΠΑΧΑΡΑΚΗ – Τράπεζα Θεμάτων Μαθηματικά Κατεύθυνσης Β’

Σε ορθοκανονικό σύστημα αξόνων Οxy θεωρούμε τα σημεία









 





Α λ 1,λ 2 και Β μ 3,μ , λ, μ .

α.

Να αποδείξετε ότι τα σημεία Α, Β κινούνται στις ευθείες

 

ε : y x 3

και

 

ε : y x 3

αντίστοιχα.

(Μονάδες 12)

β.

Να βρεθεί η εξίσωση της μεσοπαράλληλης των ευθειών

(Μονάδες 13)

Απάντηση:

α.

Είναι:

x λ 1 λ x

    

και

A A

y λ 2 x 1 2 y x 3.

       

Αφού οι συντεταγμένες του Α επαληθεύουν την εξίσωση

x 3

 

, το Α

κινείται στην ευθεία

Είναι:

x μ 3 μ x

    

και

B B

y μ x 3 y

x 3.

     

Αφού οι συντεταγμένες του Β επαληθεύουν την εξίσωση

x 3

 

, το Β

κινείται στην ευθεία

β.

Έστω

 

M x,y

σημείο της μεσοπαράλληλης. Τότε:



 



 

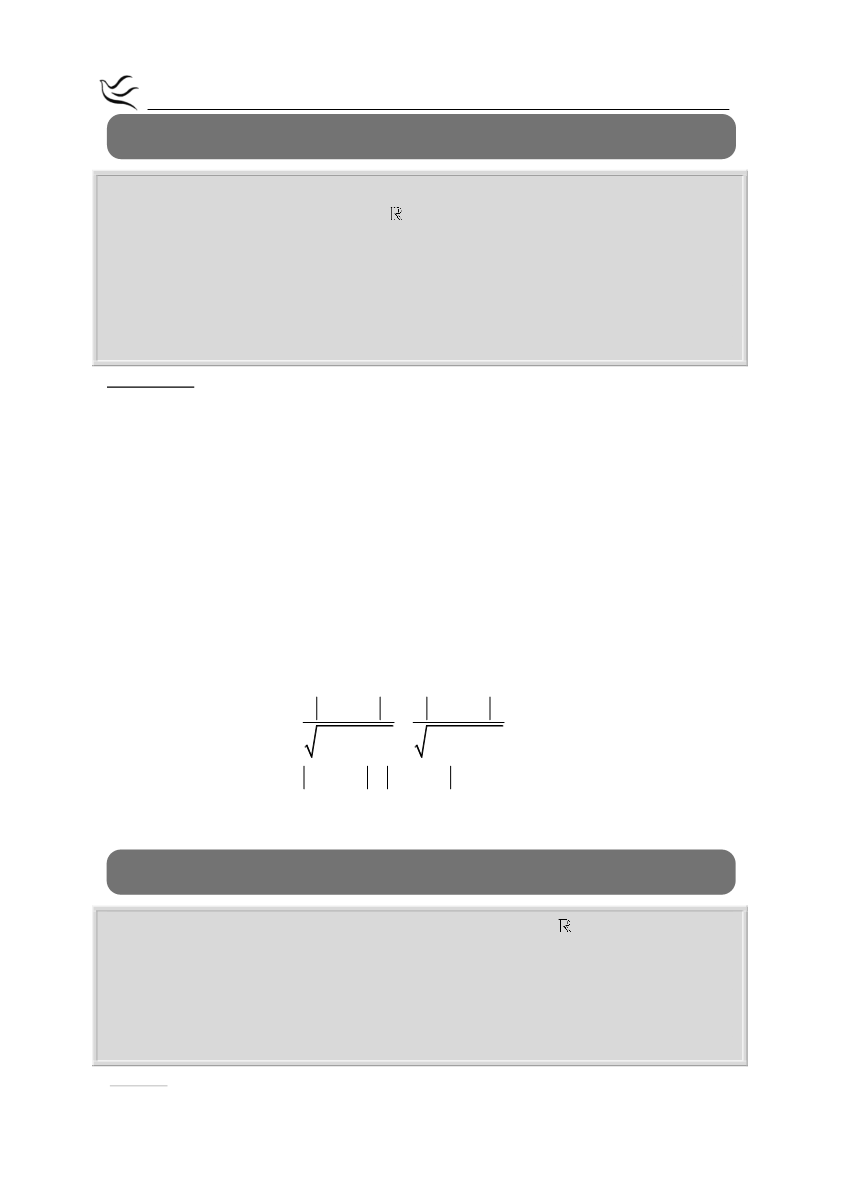
x y 3

d M,ε d M,ε

1 1 1 1

x y 3 x y 3

x y 3 x y 3 αδύνατο ή x - y 3

x y 3 y x

 

 



 

 

     

      

Δίνονται τα σημεία





 





A 0,2 , B 1,5 και Γ t 1,3t 2 , t .

 



α.

Να βρείτε την εξίσωση της ευθείας ΑΒ.

(Μονάδες 7)

β.

Να δείξετε ότι η απόσταση του σημείου Γ από την ευθεία ΑB καθώς και το

εμβαδόν του τριγώνου ΑΒΓ είναι ανεξάρτητα του t.

(Μονάδες 18)

ΘΕΜΑ 2 - 22537

ΘΕΜΑ 2 - 22538