Μαθηματικά Β' Λυκείου (Τράπεζα Θεμάτων)

63 / 130

Εκδόσεις ΜΠΑΧΑΡΑΚΗ – Τράπεζα Θεμάτων Μαθηματικά Κατεύθυνσης Β’
62
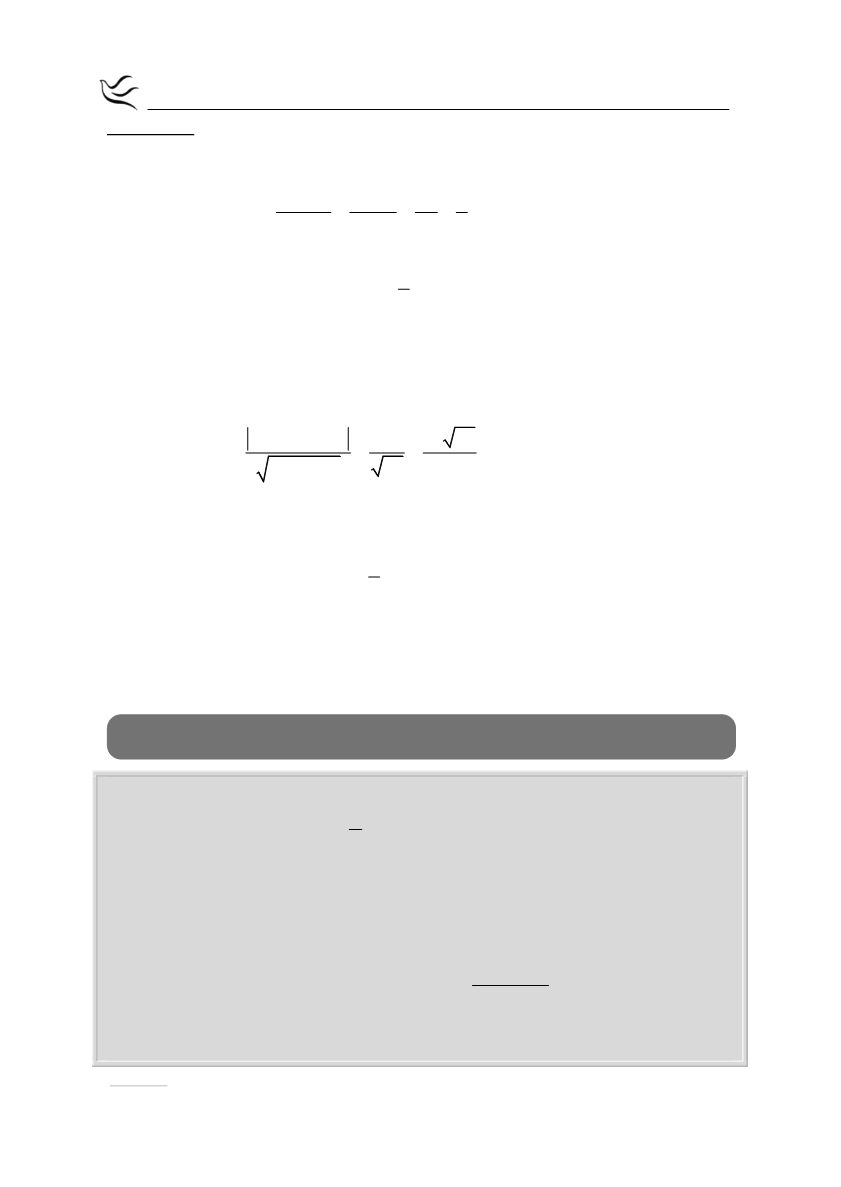
Απάντηση:
α. Έχουμε εξίσωση ευθείας που ορίζεται από δύο σημεία και επειδή 
Α Β x x ,
θα πάρουμε:
  
   
   
Β Α
ΑΒ
Β Α
y y 1 2 1 1
λ
x x 3 3 6 6
, οπότε έχουμε:
                    
Α ΑΒ Α
1
(ΑΒ):y y λ x x y 2 x 3 6y 12 x 3 x 6y 9 0
6
β. Το μήκος (ΓΔ) παρατηρούμε ότι παριστάνει την απόσταση του σημείου Γ
από την ευθεία ΑΒ, οπότε
   
   
  2 2
4 1 6 0 9 13 13 37
(ΓΔ) d(Γ,ΑΒ)
37 37 1 ( 6)
.
Για την εξίσωση του ύψους ΓΔ παίρνουμε:
           
ΓΔ ΑΒ ΓΔ ΓΔ
1
ΓΔ ΑΒ λ λ 1 λ 1 λ 6
6
Επομένως η ευθεία ΓΔ έχει εξίσωση:
                Γ ΓΔ Γ y y λ (x x ) y 0 6(x 4) y 6x 24 6x y 24 0 .
Θεωρούμε τα σημεία A(α,0) και Β(0,β), όπου   α β 0 και  α β
α. Να αποδείξετε ότι   
β
ΑΒ: y x β
α
(Μονάδες 7)
β. Αν ε είναι η ευθεία που διέρχεται από το σημείο Μ(α,β) και είναι κάθετη
προς την ευθεία ΑΒ, τότε:
i. να βρείτε την εξίσωση της ε. (Μονάδες 9)
ii. αν η ευθεία ε τέμνει τον άξονα x΄x στο σημείο Κ και τον άξονα y΄y στο
σημείο Λ, να αποδείξετε ότι
 


2
2 2
α β
(ΟΚΛ)
2αβ
,όπου O είναι η αρχή
των αξόνων.
(Μονάδες 9)
ΘΕΜΑ 2 - 22506