Μαθηματικά Β' Λυκείου (Τράπεζα Θεμάτων)

61 / 130

Εκδόσεις ΜΠΑΧΑΡΑΚΗ – Τράπεζα Θεμάτων Μαθηματικά Κατεύθυνσης Β’
60
δ.
 
   
        
 
 
    
         
1
2
ε : y x 1 y x 1 y 3
x 4 x 2 x 1 2 ε : x 2y 2
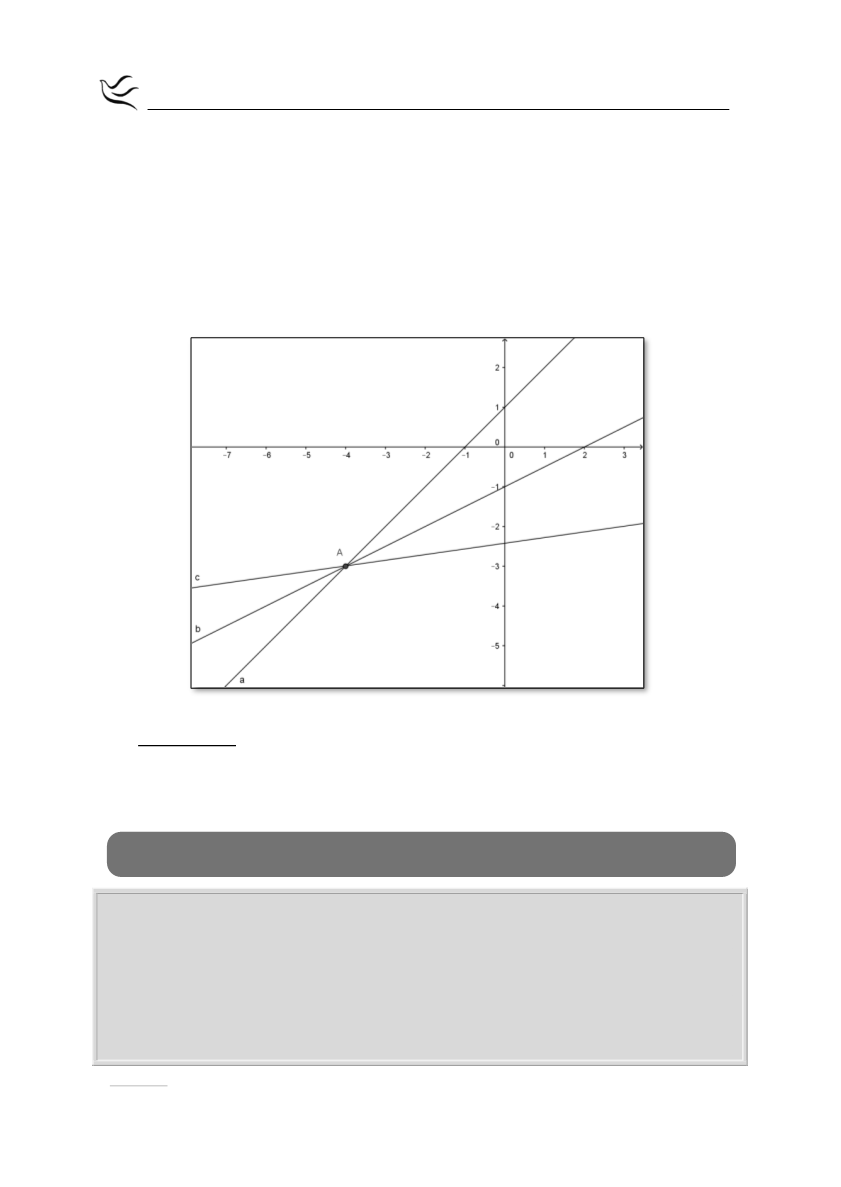
Άρα το κοινό σημείο των  
1 ε και  
2 ε είναι το  
  Α 4, 3 .
Οι συντεταγμένες του Α επαληθεύουν την εξίσωση της  
3 ε , αφού
 
          4 7 3 17 0 4 21 17 0 που ισχύει.
Επομένως οι ευθείες  
1 ε ,  
2 ε και  
3 ε συντρέχουν στο Α.
Αιτιολόγηση: Το σημείο     Α 4, 3 είναι το κοινό σημείο των  
1 ε και  2 ε .
Το συμμετρικό του Α ως προς την  2 ε είναι το Α. Επομένως το Α ανήκει στην
 3 ε και άρα οι ευθείες  1 ε ,  
2 ε και  
3 ε συντρέχουν στο Α.
Δίνονται τα σημεία    
 Α 1, 2 και B 2,3 .
α. Να βρείτε την εξίσωση της ευθείας ε που διέρχεται από τα σημεία Α, Β.
(Μονάδες 11)
β. Να υπολογίσετε το εμβαδόν του τριγώνου ΟΚΛ, όπου Ο είναι η αρχή των
αξόνων και Κ, Λ είναι τα σημεία τομής της ε με τους άξονες   x x και y y
αντίστοιχα. (Μονάδες 14)
ΘΕΜΑ 2 - 20062