Μαθηματικά Β' Λυκείου (Τράπεζα Θεμάτων)

46 / 130

45
Τράπεζα Θεμάτων Μαθηματικά Κατεύθυνσης Β’ – Εκδόσεις ΜΠΑΧΑΡΑΚΗ
  y 1 2 x 2 y 2x 4 1 y 2x 3.          
β. Αν     Α x,y το συμμετρικό του Α ως προς την ευθεία  ε , είναι:
                         ΑΜ ΜΑ 2 6,1 1 x 2, y 1 4, 2 x 2, y 1
 
      
     
  
 
x 2 4 x 2
Α 2,3 .
y 1 2 y 3
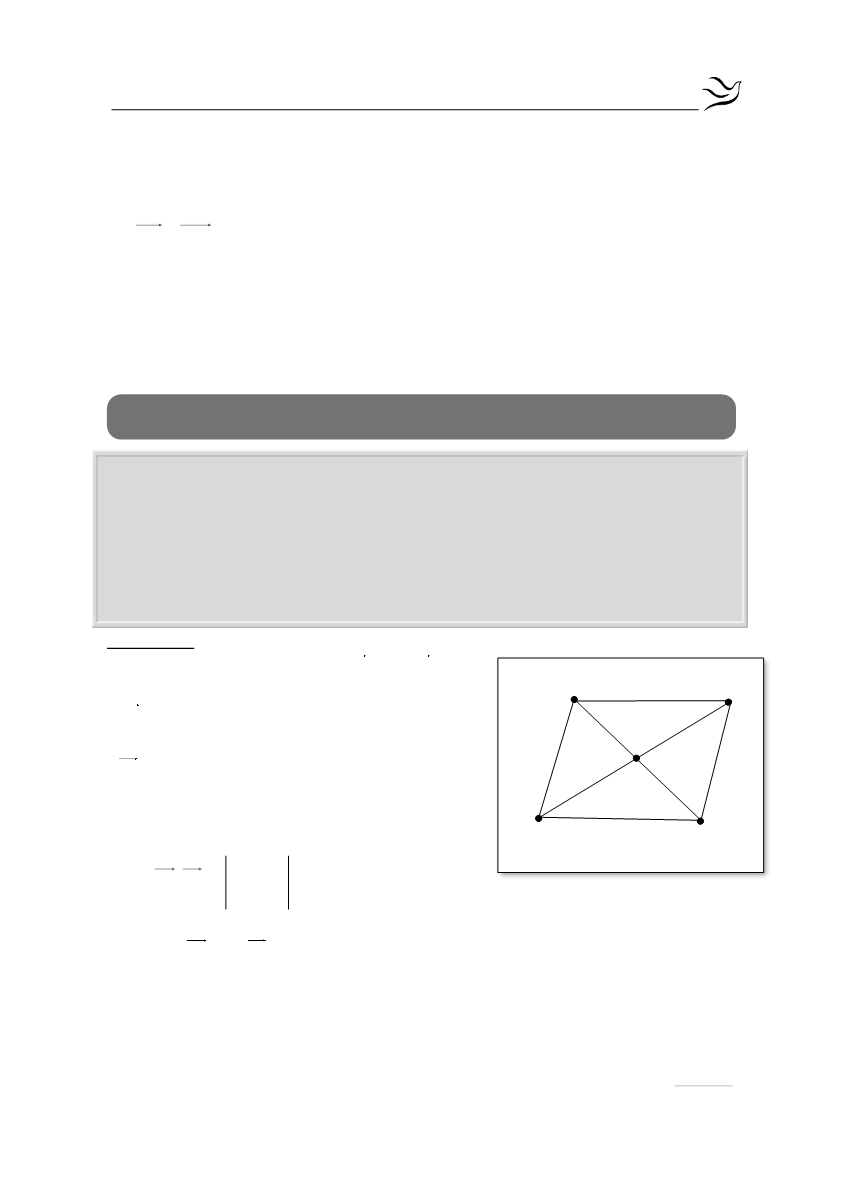
Δίνονται τα σημεία Α(2,3) , Β(1,5) και Γ(2,4).
α. Να αποδείξετε ότι σχηματίζουν τρίγωνο.
(Μονάδες 8)
β. Να βρείτε το συμμετρικό Δ του Β ως προς το μέσο Μ της ΑΓ.
(Μονάδες 10)
γ. Τι σχήμα είναι το ΑΒΓΔ; Να αιτιολογήσετε τον ισχυρισμό σας.
(Μονάδες 7)
Απάντηση:
α. Βρίσκουμε τα διανύσματα AB και AΓ .
        
Β Α Β Α AB (x x ,y y ) ( 1 2,5 3) ( 3,2)
          Γ Α Γ Α AΓ (x x ,y y ) ( 2 2, 4 3) ( 4, 7)
Παρατηρούμε ότι

    
 
3 2
det(AB,AΓ) 21 8 29 0
4 7
.
Άρα τα AB και AΓ είναι μη συγγραμμικά και επομένως τα Α,Β,Γ
σχηματίζουν τρίγωνο.
β. Το σημείο Μ είναι μέσο της ΑΓ άρα:
ΘΕΜΑ 2 - 20073
Γ(-2,4) Β(-1,5)
Α(2,3)
M
Δ