Μαθηματικά Β' Λυκείου (Τράπεζα Θεμάτων)

45 / 130

Εκδόσεις ΜΠΑΧΑΡΑΚΗ – Τράπεζα Θεμάτων Μαθηματικά Κατεύθυνσης Β’
44
Όμως  
  M M AM x 5,y 4 , άρα
    
M M x 5 1 x 4 και
   
M M
1 9
y 4 y
2 2
.
Επομένως
 
 
 
9
M 4,
2
.
γ. Ο συντελεστής διεύθυνσης της ΓΜ
είναι

  
  ΓΜ
9
1
7
2 λ
4 4 16
.
Άρα η εξίσωση της ΓΜ είναι:          
7
y 1 x 4 7x 16y 44 0
16
.
Θεωρούμε μια ευθεία (ε) και ένα σημείο Α(6, 1) εκτός της (ε).
Έστω Μ(2,1) η προβολή του Α στην (ε). Να βρείτε:
α. Την εξίσωση της ευθείας (ε).
(Μονάδες 13)
β. Το συμμετρικό του Α ως προς την (ε).
(Μονάδες 12)
Απάντηση:
α. Ο συντελεστής διεύθυνσης της ευθείας ΑΜ είναι :
 
 
   
  ΑΜ
1 1 2 1
λ .
2 6 4 2
Επειδή το σημείο Μ είναι η προβολή του Α στην ευθεία (ε) είναι:    ε ΑΜ,
οπότε:
 
         
 
 
ε ΑΜ ε ε
1
λ λ 1 λ 1 λ 2.
2
Η ευθεία  ε διέρχεται από το σημείο   Μ 2,1 και έχει συντελεστή
διεύθυνσης 
ε λ 2, οπότε η εξίσωση της είναι :
ΘΕΜΑ 2 - 20072
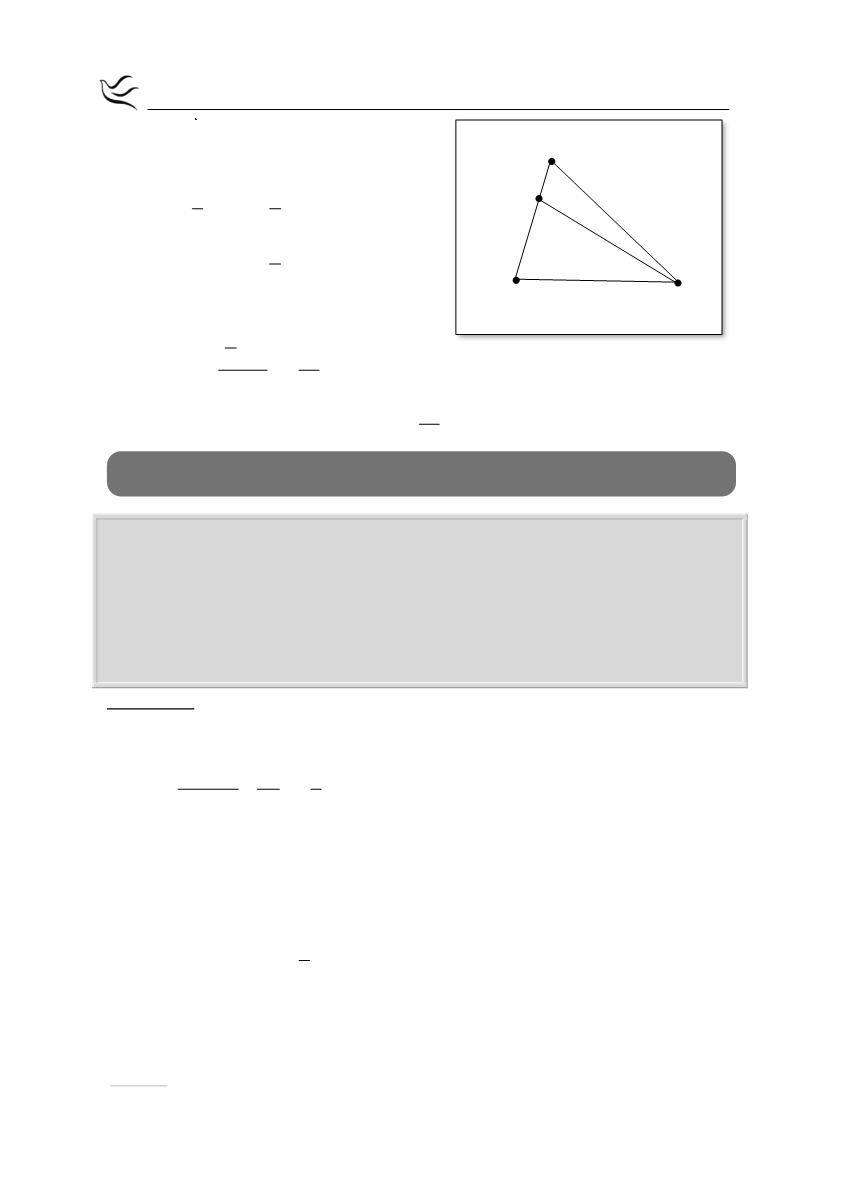
Γ(4,1) Β(-1,6)
Α(-5,4)
M