Μαθηματικά Β' Λυκείου (Τράπεζα Θεμάτων)

43 / 130

Εκδόσεις ΜΠΑΧΑΡΑΚΗ – Τράπεζα Θεμάτων Μαθηματικά Κατεύθυνσης Β’
42
   
  
1 A η Α y –y λ x –x y –1 1 x –5 x –y –4 0 .
β. Η ευθεία 2 η , η οποία διέρχεται από το Α και είναι παράλληλη προς τον
άξονα x΄x , είναι της μορφής:      
2 Α η y y y 1 .
γ. Το σημείο τομής των ευθειών 1 η και 2 η είναι προφανώς το σημείο Α
και η απόσταση του σημείου Α από την αρχή των αξόνων είναι:
    2 2 2 2
A A OA x y 5 1 26 .
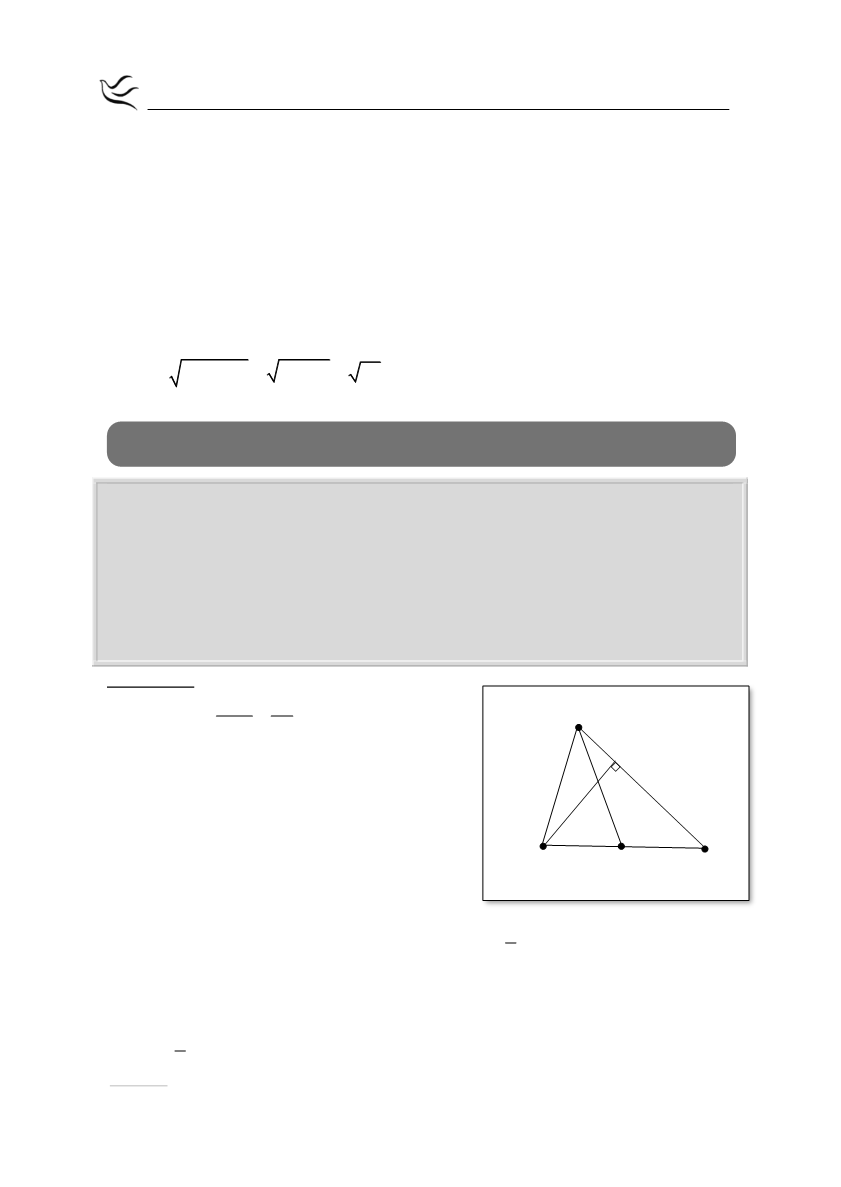
Δίνεται τρίγωνο ΑΒΓ με κορυφές τα σημεία Α(3,1) , Β( 1,1) και Γ(2,4).
α. Να βρείτε την εξίσωση της πλευράς ΑΓ.
(Μονάδες 7)
β. Να βρείτε τις εξισώσεις του ύψους ΒΔ και της διαμέσου ΑΜ.
(Μονάδες 18)
Απάντηση:
α. Είναι

   
  ΑΓ
4 1 3
λ 3
2 3 1
, οπότε η
πλευρά ΑΓ θα έχει εξίσωση:
  y 1 3 x 3 y 1 3x 9
3x y 10 0
         
  
β. Είναι :
 
           
ΒΔ ΑΓ ΒΔ ΒΔ
1
ΒΔ ΑΓ λ λ 1 λ 3 1 λ
3
.
Άρα το ύψος ΒΔ θα έχει εξίσωση:
 
             
1
y 1 x 1 3y 3 x 1 x 3y 4 0
3
.
ΘΕΜΑ 2 - 20066
Γ(2,4) Β(-1,1)
Α(3,1)
M
Δ