Μαθηματικά Β' Λυκείου (Τράπεζα Θεμάτων)

23 / 130

Εκδόσεις ΜΠΑΧΑΡΑΚΗ – Τράπεζα Θεμάτων Μαθηματικά Κατεύθυνσης Β΄
22
Απάντηση:
α. Επειδή β προβ α / /β προκύπτει ότι 
β προβ α λβ ,  λ .
Επιπλέον, ισχύει:
 2
β
3 1
α β β προβ α 2 β (λβ) λ|β|
2 2
        

 
     
 
2
2 2 1 1 5
|β| 1 1
2 4 4
Άρα
1 5 2
λ λ
2 4 5
   ,
Τελικά
   
   
  
    β
2 1 2 1
προβ α λβ 1, ,
5 2 5 5
.
β. Έστω  1 2 α α α με 
1 2 α α και 1 α / /β , άρα
 
   
 
1 β
2 1
α προβ α ,
5 5
που υπολογίσαμε στο α) ερώτημα,
Επομένως,
   
      
   
   
2 1
2 1 8 16
α α α (2, 3) , ,
5 5 5 5
.
Τελικά οι δύο συνιστώσες είναι :  
   
 
1 β
2 1
α προβ α ,
5 5
και 2
8 16
α ,
5 5
 
  
 
.
Δίνονται τα διανύσματα   α (2, 3) και 
1
β (1, )
2
.
α. Να βρείτε την προβολή του α πάνω στο β .
(Μονάδες 10)
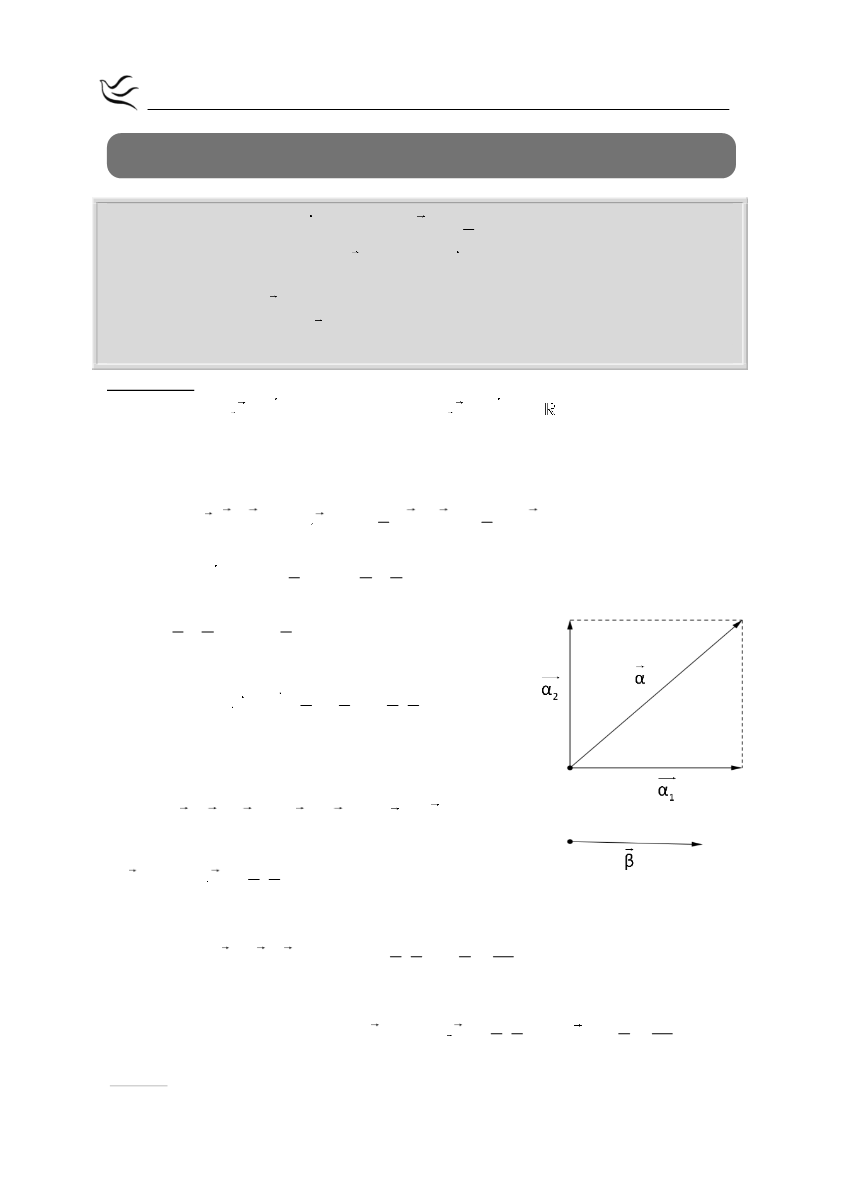
β. Να αναλύσετε το α σε δύο κάθετες συνιστώσες από τις οποίες η μία να
είναι παράλληλη με το β .
(Μονάδες 15)
ΘΕΜΑ 2 - 20069