Εκδόσεις ΜΠΑΧΑΡΑΚΗ – Τράπεζα Θεμάτων Μαθηματικά Κατεύθυνσης Β΄
26
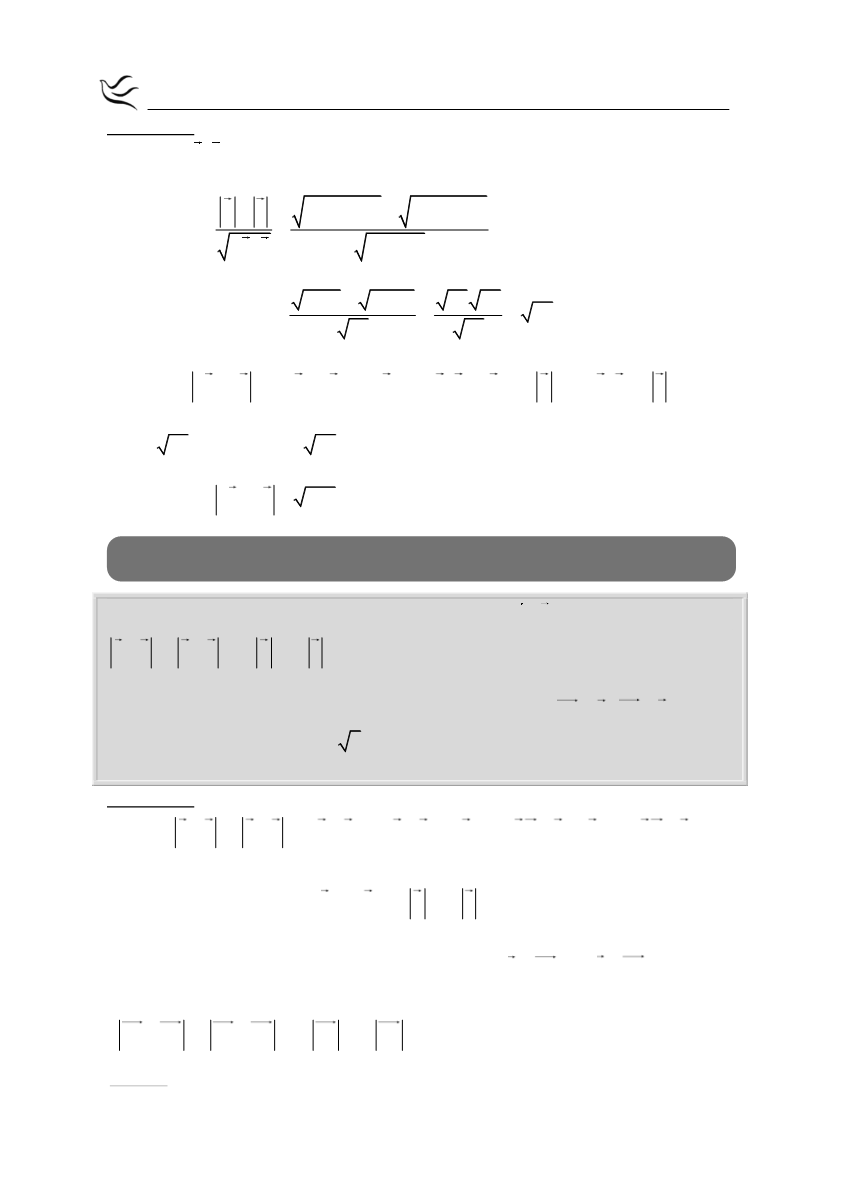
Απάντηση:
α.
Έχουμε
α β 2, 3 5,1 2 5 3 1 10 3 13
Επομένως
2
2
2
2
α β 2 3
5 1
13
α β
4 9
25 1 13 26
26
13
13
β.
Έχουμε
2
2
2
2
2
2
2α 3β 2α 3β
4α 12α β 9β 4 α
12α β 9 β
2
2
4 13 12 13
9 26 4 13 12 13 9 26 52 156 234 442
Επομένως
2α 3β 442
.
α.
Να αποδείξετε ότι για οποιαδήποτε διανύσματα
α
,
β
ισχύει:
2
2
2
2
α β α β 2 α 2 β
.
(Μονάδες 12)
β.
Δίνεται ρόμβος ΑΒΓΔ με πλευρά ίση με τη μονάδα και
ΑΒ α
,
ΑΔ β
. Αν η
διαγώνιός του ΑΓ έχει μήκος
3
, να βρείτε το μήκος της διαγώνιου ΒΔ.
(Μονάδες 13)
Απάντηση:
α.
Είναι
2
2
2
2
2
2
2
2
α β α β α β α β α 2 α β β α 2 α β β
2
2
2
2
2α 2β 2 α 2 β
.
β.
Αντικαθιστώντας στη σχέση του α) ερωτήματος
α ΑΒ
και
β ΑΔ
βρίσκουμε :
2
2
2
2
ΑΒ ΑΔ ΑΒ ΑΔ 2 ΑΒ
2 ΑΔ
ΘΕΜΑ 2 - 22527









