Εκδόσεις ΜΠΑΧΑΡΑΚΗ – Τράπεζα Θεμάτων Μαθηματικά Κατεύθυνσης Β΄
12
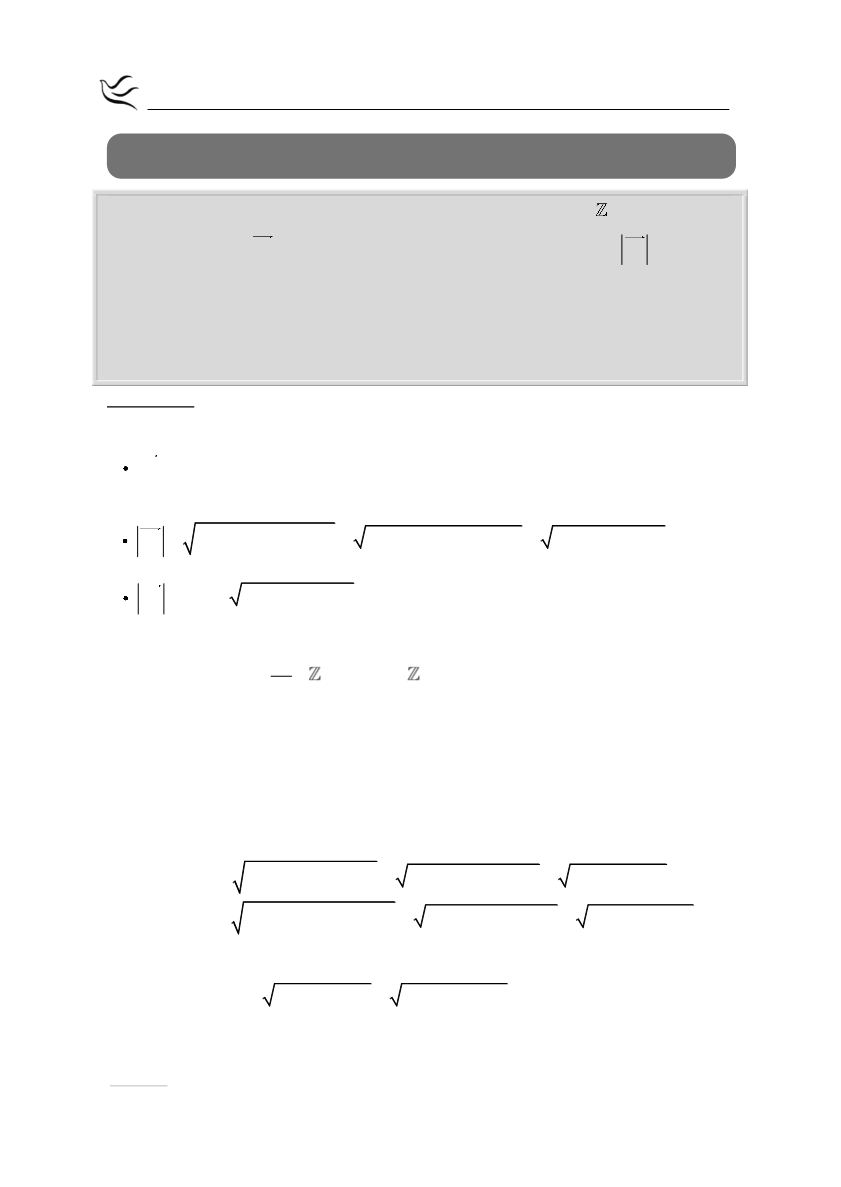
Θεωρούμε τα σημεία
Α 1 2α, 4α 2
και
Β 5α 1, α
,
α
α.
Να γράψετε το
AB
συναρτήσει του α και να βρείτε το α ώστε
AB 10
.
(Μονάδες 12)
β.
Έστω
α 2.
Να βρείτε σημείο Μ του άξονα x΄x ώστε το τρίγωνο MAB να
είναι ισοσκελές με βάση την AB.
(Μονάδες 13)
Απάντηση:
α.
Έχουμε:
AB 5α 1 1 2α , α 4α 2 5α 1 1 2α, α 4α 2
3α, 5α 2
2
2
2
2
2
AB 3α 5α 2 9α 25α 20α 4 34α 20α 4
2
2
2
2
AB 10 34α 20α 4 10 34α 20α 4 100
34α 20α 96 0 17α 10α 48 0
24
α
ή α 2
7
Επομένως
α 2
.
β.
Έστω
Μ x,0
σημείο του άξονα
x x.
Για
α 2,
βρίσκουμε
A 5,6
και
Β 11, 2
. Επιπλέον:
2
2
2
2
ΜΑ 5 x 6 0 x 10x 25 36 x
10x 61
2
2
2
2
ΜB 11 x
2 0 x 22x 121 4 x 22x 125
Για να είναι το τρίγωνο
ΜΑΒ
ισοσκελές με βάση την
ΑΒ,
πρέπει να ισχύει:
2
2
ΜΑ ΜΒ x
10x 61 x
22x 125
ΘΕΜΑ 2 - 20071









