Μαθηματικά Β' Λυκείου (Τράπεζα Θεμάτων)

10 / 130

9
Τράπεζα Θεμάτων Μαθηματικά Κατεύθυνσης Β΄- Εκδόσεις ΜΠΑΧΑΡΑΚΗ
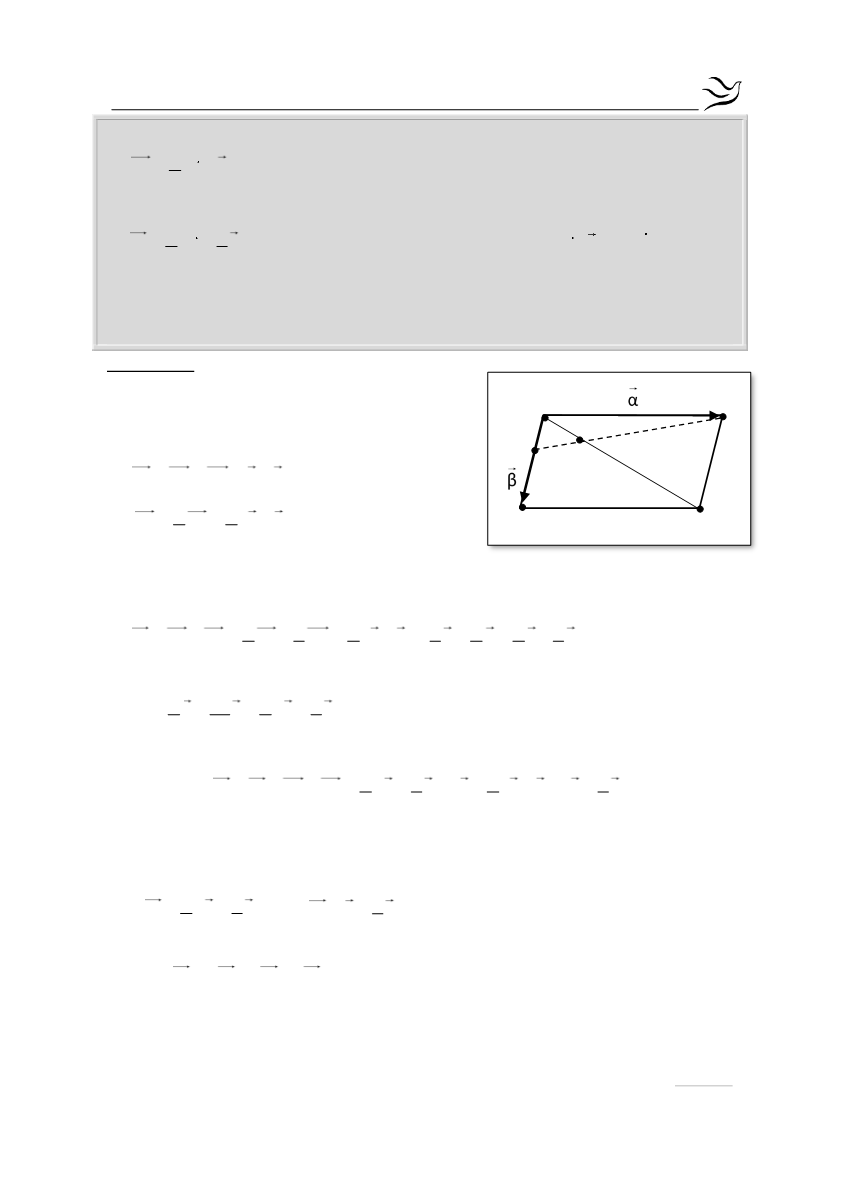
Να αποδείξετε ότι:
α.  
 
1
ΑΖ α β
4
(Μονάδες 8)
β.
 
  
 
1 1
ΕΖ α β
4 3
και να υπολογίσετε με τη βοήθεια των α , β το ΕΒ .
(Μονάδες 12)
γ. Tα σημεία Ε,Ζ,Β είναι συνευθειακά.
(Μονάδες 5)
Απάντηση:
α. Για τη διαγώνιο ΑΓ του
παραλληλόγραμμου γνωρίζουμε ότι:
    ΑΓ ΑΒ ΑΔ α β , οπότε
 
  
1 1
ΑΖ ΑΓ α β
4 4
.
β. Παίρνοντας ως σημείο αναφοράς το Α έχουμε:
 
          
1 1 1 1 1 1 1
ΕΖ ΑΖ ΑΕ ΑΓ ΑΔ α β β α β β
4 3 4 3 4 4 3
 
    
 
1 1 1 1
α β α β
4 12 4 3
.
Έπιπλέον   1 1 1 1
ΕΒ ΕΖ ΑΒ ΑΖ α β α α β α β
4 3 4 3
 
          
 
.
γ. Σύμφωνα με το β ερώτημα ισχύει :
 
  
 
1 1
ΕΖ α β
4 3
και
1
ΕΒ α β
3
 
Άρα ΕΒ 4ΕΖ ΕΒ / /ΕΖ   και Ε κοινο σημείο ,επομένως
τα σημεία Ε,Ζ,Β είναι συνευθειακά.
Γ
Β
Α
Δ
Ε Ζ