Εκδόσεις ΜΠΑΧΑΡΑΚΗ – Τράπεζα Θεμάτων Μαθηματικά Κατεύθυνσης Β΄
6
Δίνεται τρίγωνο ΑΒΓ και σημεία Δ και Ε του επιπέδου τέτοια, ώστε
ΑΔ 2ΑΒ 5ΑΓ
και
ΑΕ 5ΑΒ 2ΑΓ
α.
Να γράψετε το διάνυσμα
ΔΕ
ως γραμμικό συνδυασμό των
ΑΒ
και
ΑΓ
.
(Μονάδες 13)
β.
Να δείξετε ότι τα διανύσματα
ΔΕ
και
ΒΓ
είναι παράλληλα.
(Μονάδες 12)
Απάντηση:
α.
Θεωρώντας ως σημείο αναφοράς το Α, βρίσκουμε:
ΔΕ ΑΕ ΑΔ 5ΑΒ 2ΑΓ (2ΑΒ 5ΑΓ) 5ΑΒ 2ΑΓ 2ΑΒ 5ΑΓ
3ΑΒ 3ΑΓ
β.
Έχουμε:
ΔΕ 3ΑΒ 3ΑΓ 3(ΑΒ ΑΓ) 3ΓΒ 3ΒΓ
, άρα
ΔΕ ΒΓ
.
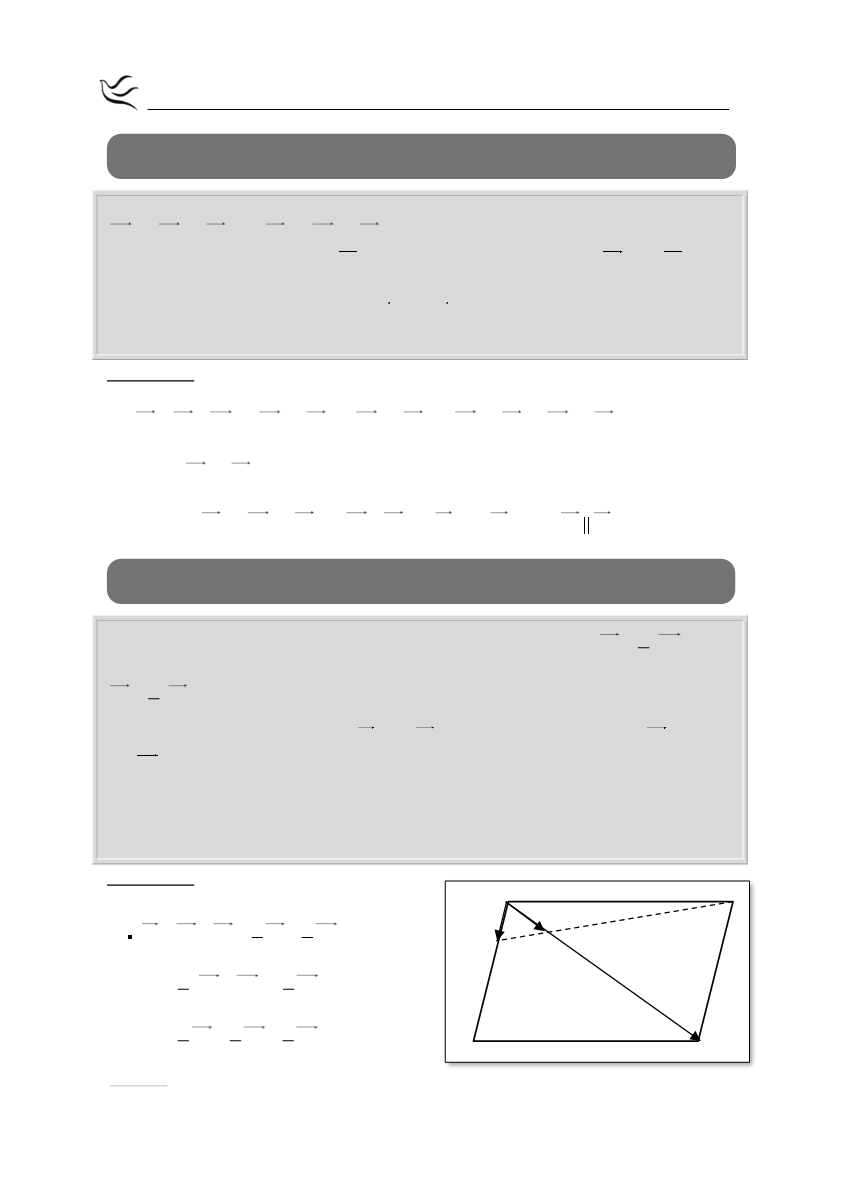
Δίνεται παραλληλόγραμμο ΑΒΓΔ και E , Z σημεία τέτοια ώστε:
2
ΑΕ ΑΔ
5
και
2
ΑΖ ΑΓ
7
.
α.
Να γράψετε τα διανύσματα
ΕΖ
και
ΖΒ
ως γραμμικό συνδυασμό
ΑΒ
και
ΑΔ
.
(Μονάδες 13)
β.
Να αποδείξτε ότι τα σημεία B , Z και E είναι συνευθειακά.
(Μονάδες 12)
Απάντηση:
α.
Έχουμε:
2 2
ΕΖ ΑΖ ΑΕ ΑΓ ΑΔ
7 5
2
2
ΑΒ ΑΔ ΑΔ
7
5
2 2 2
ΑΒ ΑΔ ΑΔ
7 7 5
ΘΕΜΑ 2 –
_
18603
ΘΕΜΑ 2 – 18604
Α
Β
Δ
Γ
Ζ
Ε









