Γεωμετρία A' Λυκείου (Τράπεζα Θεμάτων)

99 / 226

Εκδόσεις ΜΠΑΧΑΡΑΚΗ – Τράπεζα Θεμάτων Γεωμετρίας Α’ Γενικού Λυκείου
Απάντηση:
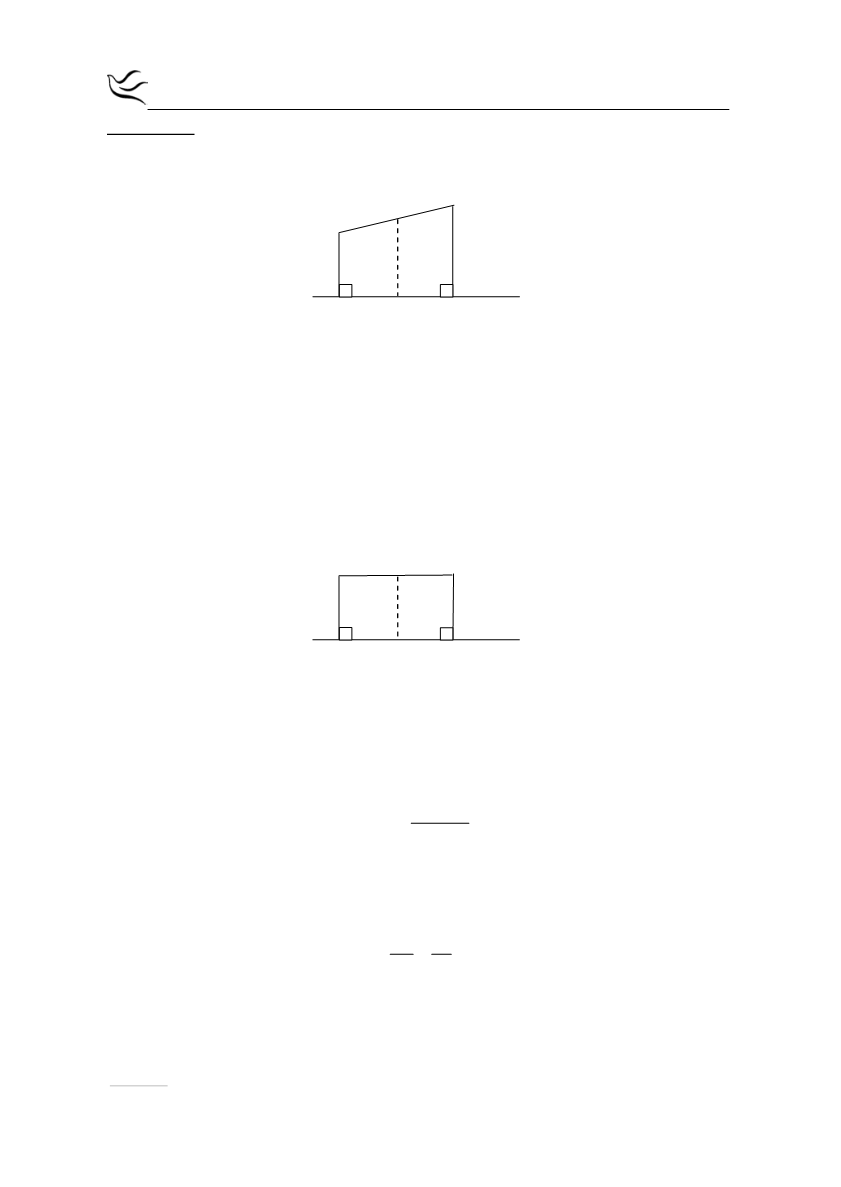
α) i) 1)
Είναι ⊥ ΑΔ ε και ⊥ ΒΓ ε . Άρα, ΑΔ//ΒΓ. Επειδή όμως οι ΑΒ και ΔΓ δεν είναι
παράλληλες το τετράπλευρο ΑΒΓΔ είναι τραπέζιο.
2) Είναι πάλι ⊥ ΑΔ ε και ⊥ ΒΓ ε . Άρα, ΑΔ//ΒΓ.
Είναι όμως ταυτόχρονα και ΑΔ=ΒΓ.
Επειδή λοιπόν ΑΔ//=ΒΓ το τετράπλευρο ΑΒΓΔ είναι παραλληλόγραμμο.
Επιπλέον, το παραλληλόγραμμο ΑΒΓΔ έχει και μία γωνία ορθή ( =  0 Γ 90 ) άρα,
θα είναι και ορθογώνιο.
ii) 1) Η ΜΝ είναι διάμεσος του τραπεζίου άρα, θα είναι
+
= ΑΔ ΒΓ
ΜΝ
2
.
2) Στο ορθογώνιο παραλληλόγραμμο ΑΒΓΔ επειδή Μ, Ν μέσα των ΑΒ και ΓΔ
αντίστοιχα θα είναι
= = =ΑΒ ΓΔ
ΑΜ ΝΔ
2 2
.
Ταυτόχρονα ΑΜ//ΝΔ άρα, το τετράπλευρο ΑΜΝΔ είναι παραλληλόγραμμο.
Συνεπώς, ΜΝ=ΑΔ=ΒΓ.
Α Β
Γ Δ
Μ
Ν ε
Α
Β
Γ Δ
Μ
Ν
ε
98