Εκδόσεις ΜΠΑΧΑΡΑΚΗ – Τράπεζα Θεμάτων Γεωμετρίας Α’ Γενικού Λυκείου
Απάντηση:
α) Φέρουμε τις ακτίνες ΟΒ και ΟΓ .
Η γωνία
ΒΑΓ
και η γωνία
ΒΟΓ
είναι εγγεγραμμένη και επίκεντρη αντίστοιχα, οι
οποίες βαίνουν στο ίδιο τόξο
ΒΓ
. Όμως
=
0
ΒΑΓ 60
επειδή το τρίγωνο ΑΒΓ είναι
ισόπλευρο. Άρα,
=
0
ΒΟΓ 120
.
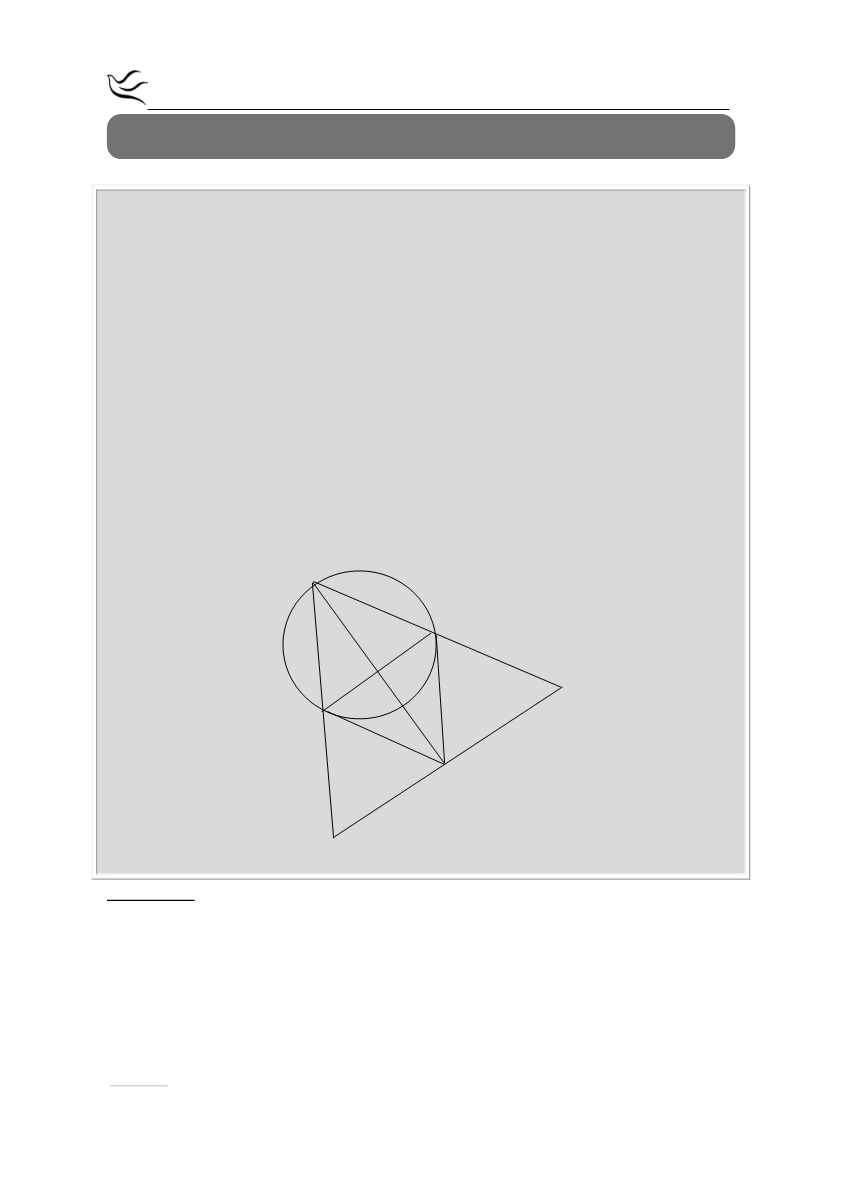
Δίνεται το ισόπλευρο τρίγωνο ΑΒΓ που είναι εγγεγραμμένο στον κύκλο με
κέντρο Ο και ακτίνα ρ. Τα τμήματα ΓΖ και ΒΖ είναι τα εφαπτόμενα τμήματα του
κύκλου στα σημεία Γ και Β αντίστοιχα. Αν το τμήμα ΘΗ είναι κάθετο στο τμήμα
ΑΖ στο Ζ, να αποδείξετε ότι:
α) το τρίγωνο ΖΒΓ είναι ισόπλευρο
(Μονάδες 7)
β) το τετράπλευρο ΑΓΖΒ είναι ρόμβος
(Μονάδες 8)
γ) το τετράπλευρο ΒΓΗΘ είναι τραπέζιο, με ΒΘ = ΒΖ και ΘΗ = 2ΒΓ.
(Μονάδες 10)
Θ
Α
Β
Ο
Η
Γ
Ε
Ζ
•
•
•
•
•
•
•
•
ΘΕΜΑ 2810
100









