Εκδόσεις ΜΠΑΧΑΡΑΚΗ – Τράπεζα Θεμάτων Γεωμετρίας Α’ Γενικού Λυκείου
Άρα,
= + = + =
0
0
0
ΒΑΔ Α ΓΑΔ 60 30 90
.
β) Επειδή
=
0
ΒΑΔ 90
.
οι ευθείες ΑΒ και ΕΔ είναι και οι δύο κάθετες στην ίδια ευθεία ΑΔ επομένως, θα
είναι ΑΒ//ΔΕ.
Ταυτόχρονα ισχύει ΑΒ=ΒΓ=ΔΕ.
Συνεπώς, ΑΒ//=ΔΕ με αποτέλεσμα το ΑΒΔΕ να είναι παραλληλόγραμμο.
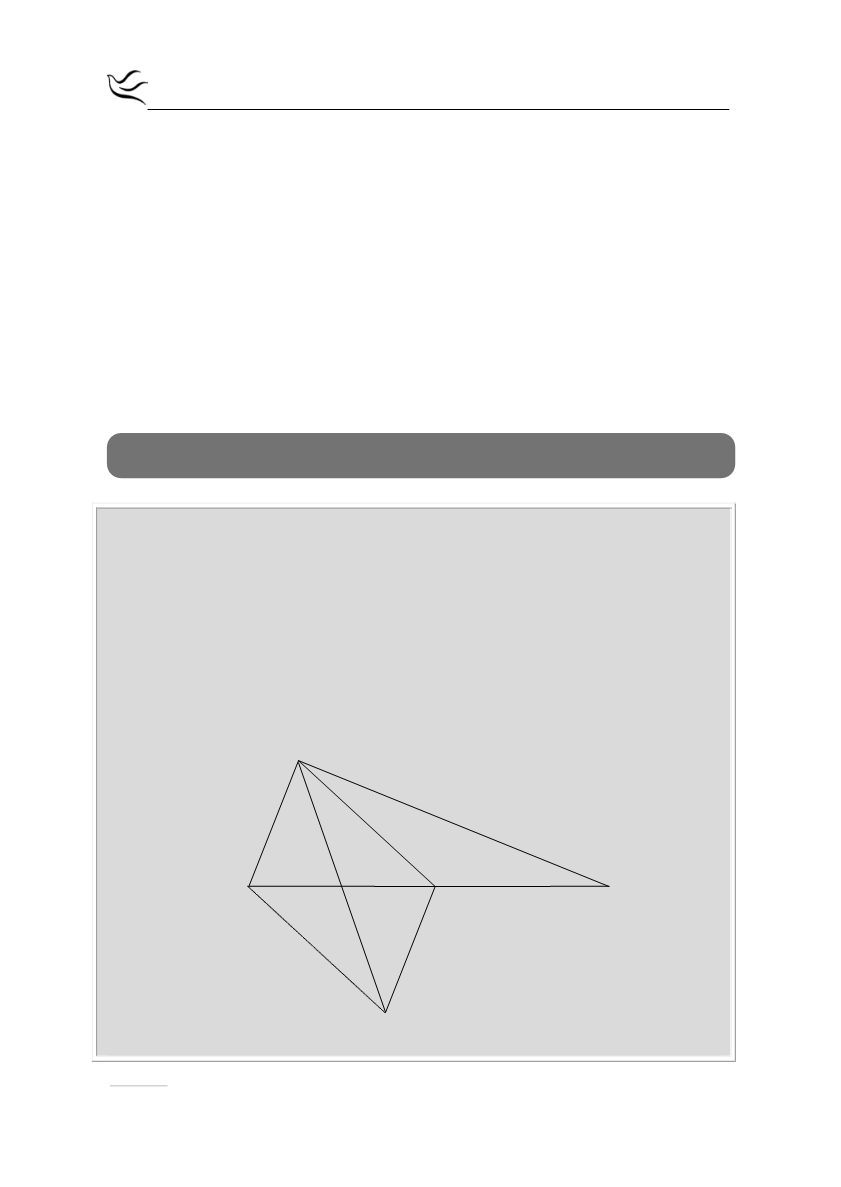
Δίνεται τρίγωνο ΑΒΓ στο οποίο ισχύει ΒΓ=2ΑΒ και έστω Μ το μέσο της ΒΓ. Αν η
ΑΔ είναι διάμεσος του τριγώνου ΑΒΜ και Ε σημείο στην προέκτασή της ώστε
ΑΔ=ΔΕ να αποδείξετε ότι:
α) το τετράπλευρο ΑΒΕΜ είναι παραλληλόγραμμο
(Μονάδες 12)
β) MΕ=ΜΓ.
(Μονάδες 13)
Β
Μ
Γ
A
Δ
Ε
ΘΕΜΑ 5574
72









