Τράπεζα Θεμάτων Γεωμετρίας Α’ Γενικού Λυκείου – Εκδόσεις ΜΠΑΧΑΡΑΚΗ
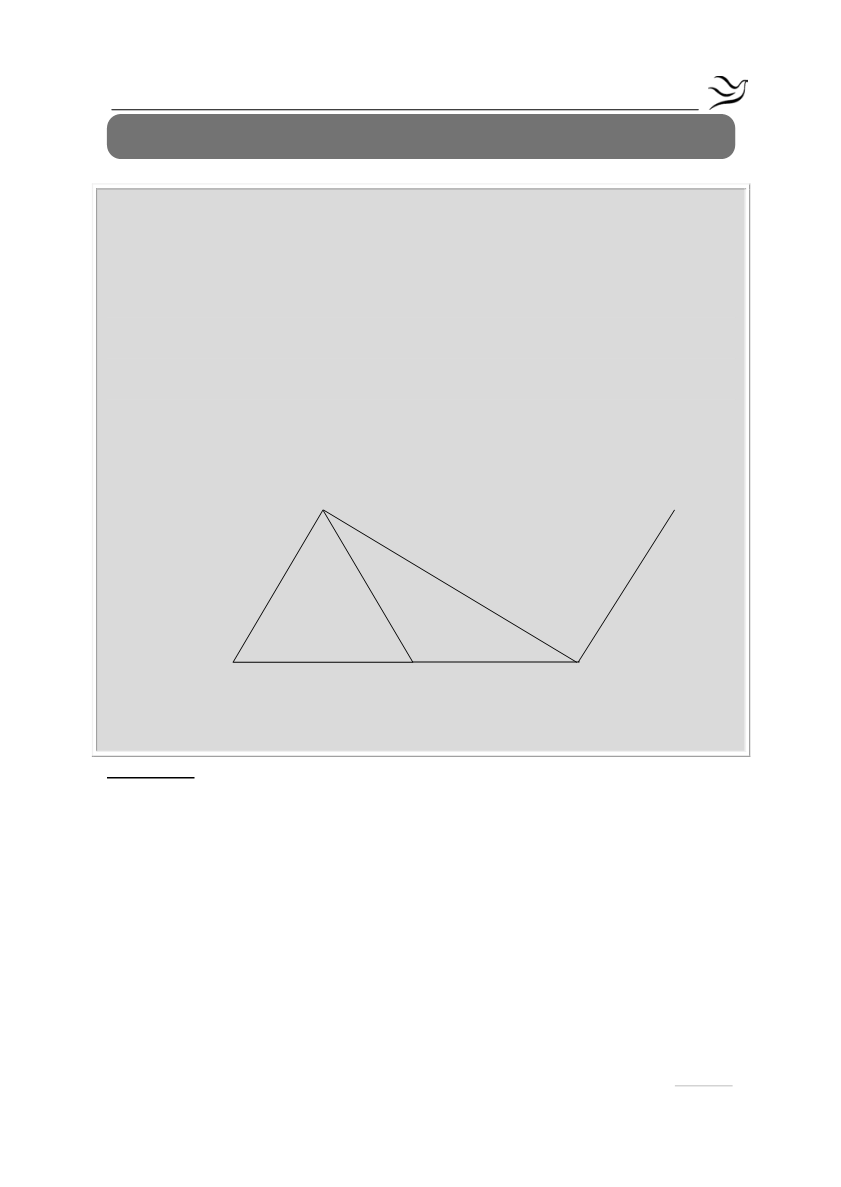
Δίνεται ισόπλευρο τρίγωνο ΑΒΓ . Στην προέκταση της ΒΓ (προς το μέρος του Γ)
θεωρούμε τμήμα
ΓΔ ΒΓ
=
. Φέρουμε τμήμα ΔΕ κάθετο στην ΑΔ στο σημείο της
Δ, τέτοιο ώστε
ΔΕ ΒΓ
=
(Α και Ε στο ίδιο ημιεπίπεδο ως προς την ΒΔ).
α) Να βρείτε τις γωνίες του τριγώνου ΑΒΔ.
(Μονάδες 12)
β) Να αποδείξετε ότι ΑΒΔΕ παραλληλόγραμμο.
(Μονάδες 13)
Απάντηση:
α) Το τρίγωνο ΑΒΓ είναι ισόπλευρο άρα,
0
Α Β Γ 60
= = =
οπότε
0
ΑΓΔ Γ 180
+ = ⇔
0
0
ΑΓΔ 60 180
+ = ⇔
0
ΑΓΔ 120
=
.
Το τρίγωνο ΑΓΔ είναι ισοσκελές αφού ΓΔ=ΒΓ=ΑΓ άρα,
ΓΑΔ ΓΔΑ
=
.
Συνεπώς, στο τρίγωνο ΑΓΔ είναι
0
ΑΓΔ ΓΑΔ ΓΔΑ 180
+ + = ⇔
+ = ⇔
0
0
120 2ΓΔΑ 180
= ⇔
0
2ΓΔΑ 60
=
0
ΓΔΑ 30
.
Ε
Β
Α
Δ
Γ
ΘΕΜΑ 5568
71









