Τράπεζα Θεμάτων Γεωμετρίας Α’ Γενικού Λυκείου – Εκδόσεις ΜΠΑΧΑΡΑΚΗ
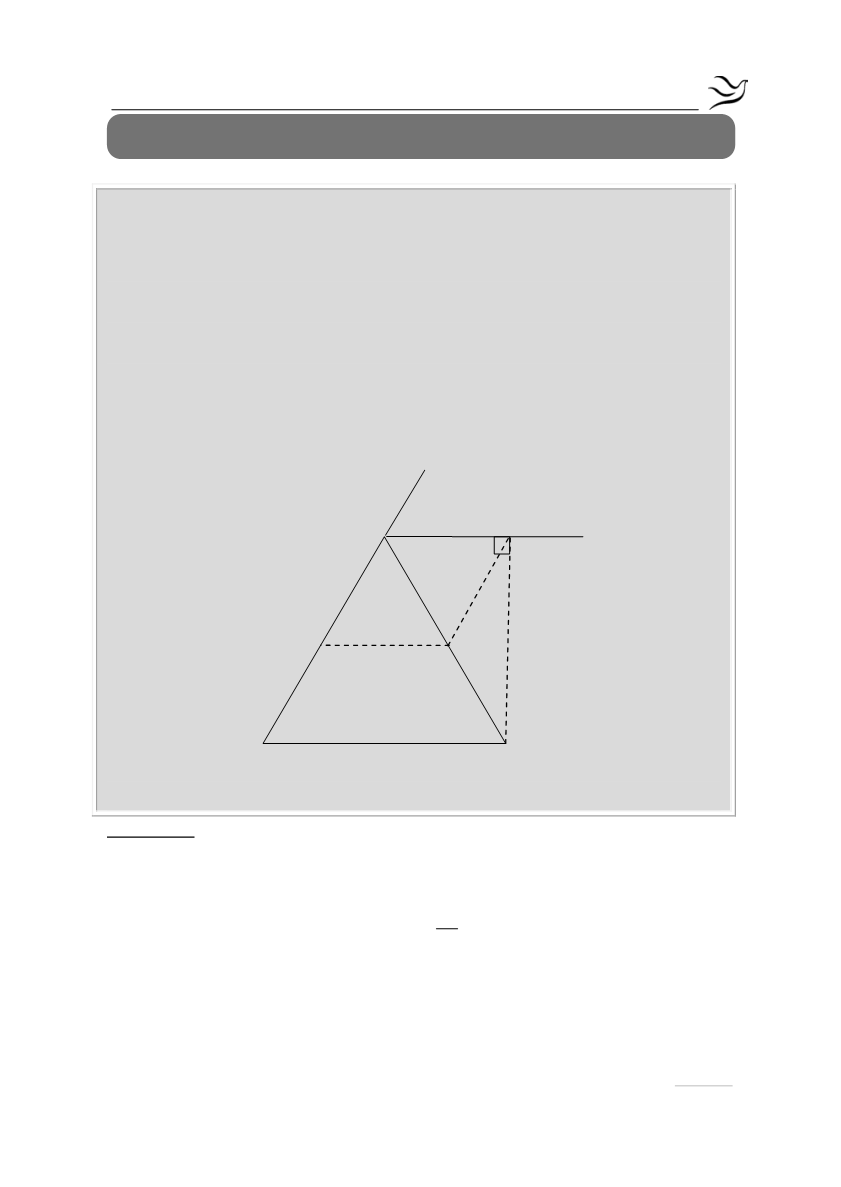
Δίνεται ισόπλευρο τρίγωνο ΑΒΓ. Φέρουμε την εξωτερική διχοτόμο Αx της
γωνίας
Α
και από το σημείο Γ την κάθετο ΓΔ στην Ax . Τα σημεία Ε και Ζ είναι
τα μέσα των πλευρών ΑΒ και ΑΓ αντίστοιχα. Να αποδείξετε ότι:
α) το τρίγωνο ΑΖΔ είναι ισόπλευρο
(Μονάδες 13)
β) το τετράπλευρο ΑΔΖΕ είναι ρόμβος .
(Μονάδες 12)
Απάντηση:
α) Στο ορθογώνιο τρίγωνο ΑΔΓ η
ΔΖ
είναι διάμεσος που αντιστοιχεί στην
υποτείνουσα ΑΓ άρα,
ΑΓ
ΔZ AZ
2
= =
(1)
Επίσης, επειδή το τρίγωνο ΑΒΓ είναι ισόπλευρο είναι
0
Α Β Γ 60
= = =
.
Β
Γ
Ε
Α
Δ
Ζ
x
ΘΕΜΑ 5149
67









