Γεωμετρία A' Λυκείου (Τράπεζα Θεμάτων)

Τράπεζα Θεμάτων Γεωμετρίας Α’ Γενικού Λυκείου – Εκδόσεις ΜΠΑΧΑΡΑΚΗ

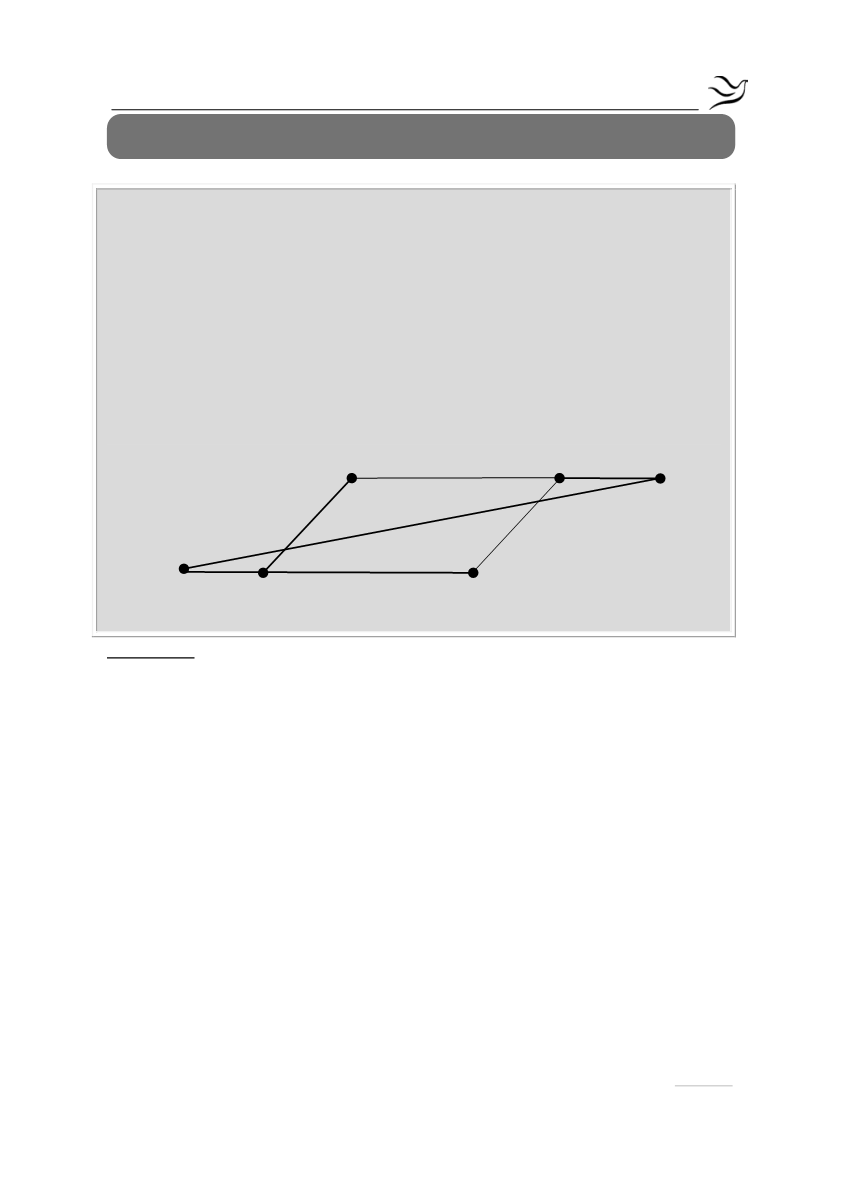
Στις πλευρές ΑΔ και ΒΓ παραλληλογράμμου ΑΒΓΔ θεωρούμε σημεία E και Z,

τέτοια, ώστε ΑE=ΓZ . Αν η ευθεία ΖΕ τέμνει τις προεκτάσεις των πλευρών ΑΒ

και ΓΔ στα σημεία H και Θ, να αποδείξετε ότι:

α)

 

ΗΒΖ ΕΔΘ

(Μονάδες 8)

β)

 

ΒΖΗ ΔΕΘ

(Μονάδες 8)

γ) ΒΗ=ΘΔ .

(Μονάδες 9)

Απάντηση:

α) Επειδή το ABΓΔ είναι παραλληλόγραμμο θα έχει τις απέναντι γωνίες του

ίσες. Έτσι θα είναι



Β Δ



οπότε θα είναι και

 

ΗΒΖ ΕΔΘ

ως παραπληρωματικές

ίσων γωνιών.

β) Είναι

 

ΓΖΕ ΑΕΖ

ως εντός εναλλάξ των παραλλήλων ΑΔ και ΒΓ που τέμνονται

από την ΕΖ. Άρα, θα είναι και

 

ΒΖΗ ΔΕΘ

ως κατακορυφήν ίσων γωνιών.

γ) Τα τρίγωνα ΒΖΗ και ΔΕΘ είναι ίσα γιατί

•

ΔΕ=ΒΖ ως διαφορές ίσων τμημάτων

•

 

ΗΒΖ ΕΔΘ

από το ερώτημα α)

•

 

ΒΖΗ ΔΕΘ

από το ερώτημα β).

Άρα, ΒΗ=ΘΔ.

●

ΘΕΜΑ 5108