Εκδόσεις ΜΠΑΧΑΡΑΚΗ – Τράπεζα Θεμάτων Γεωμετρίας Α’ Γενικού Λυκείου
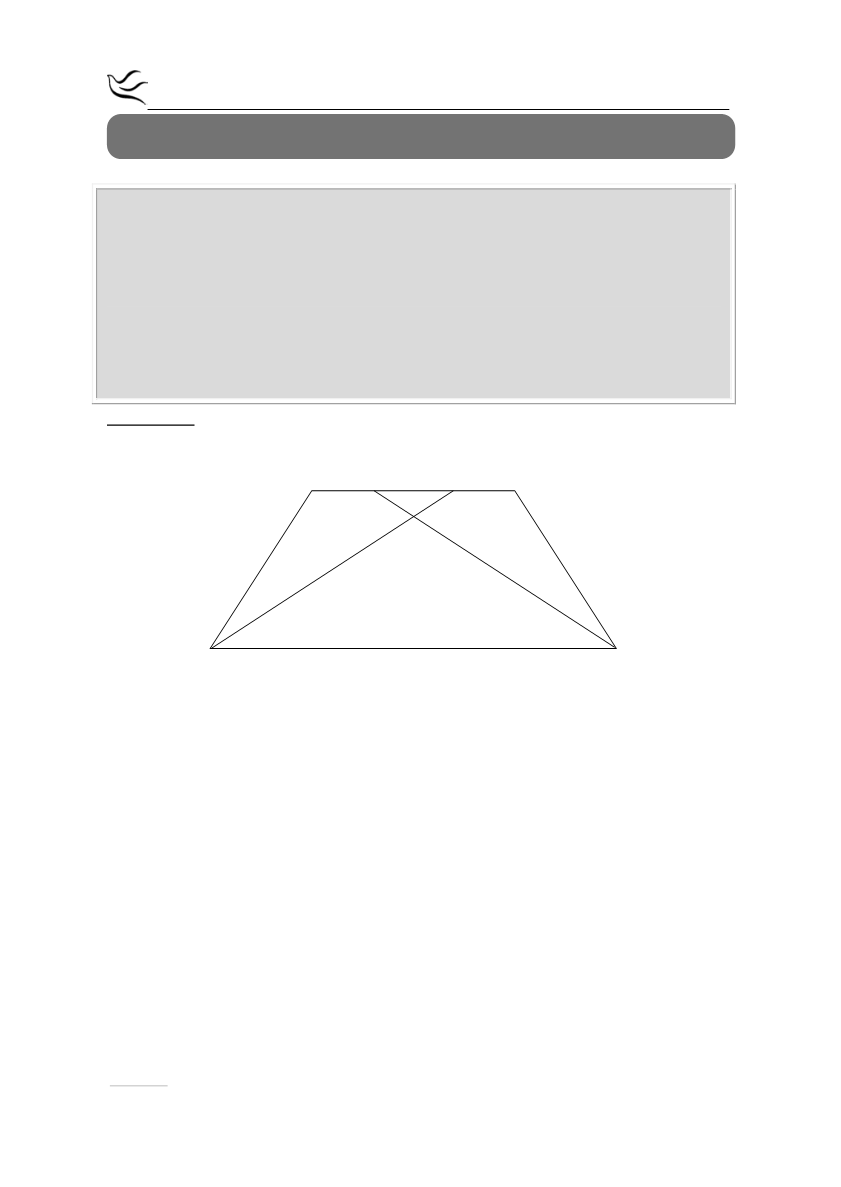
Δίνεται ισοσκελές τραπέζιο ΑΒΓΔ με ΑΒ//ΓΔ και ΑΒ<ΓΔ. Θεωρούμε τα σημεία
Ε και Ζ πάνω στην ΑΒ έτσι ώστε ΑΕ=ΕΖ=ΖΒ και έστω Κ το σημείο τομής των ΔΖ
και ΓΕ. Να αποδείξετε ότι:
α) ΔΖ=ΓΕ
(Μονάδες 13)
β) τα τρίγωνα ΕΚΖ και ΔΚΓ είναι ισοσκελή.
(Μονάδες 12)
Απάντηση:
α)
Τα τρίγωνα ΖΑΔ και ΒΕΓ είναι ίσα γιατί
•
ΑΖ=ΒΕ ως αθροίσματα ίσων τμημάτων
•
ΖΑΔ ΕΒΓ
=
επειδή ΑΒΓΔ ισοσκελές τραπέζιο
•
ΑΔ=ΒΓ επειδή ΑΒΓΔ ισοσκελές τραπέζιο.
Άρα, ΔΖ=ΓΕ.
β) Από το α) ερώτημα προκύπτει ότι
ΔΖΑ ΒΕΓ
=
άρα, το τρίγωνο ΕΚΖ είναι
ισοσκελές.
Επίσης, από το α) ερώτημα προκύπτει ότι
ΑΔΖ ΒΓΕ
=
(1).
Επειδή όμως το ΑΒΓΔ είναι ισοσκελές τραπέζιο
Δ Γ
=
(2).
Από τις σχέσεις (1) και (2) συμπεραίνουμε ότι
=
ΚΔΓ ΚΓΔ
ως διαφορές ίσων
γωνιών άρα, το τρίγωνο ΚΔΓ είναι ισοσκελές.
Β
Ε
Α
Δ
Ζ
Κ
Γ
//
//
//
―
―
ΘΕΜΑ 5007
58









