Τράπεζα Θεμάτων Γεωμετρίας Α’ Γενικού Λυκείου – Εκδόσεις ΜΠΑΧΑΡΑΚΗ
0
Ε ΓΑΕ ΑΓΕ 180
+ + = ⇔
0
2Ε 60 1800
+ = ⇔
0
2Ε 120
= ⇔
0
Ε 60
=
.
Άρα, από τις σχέσεις (1) και (2) προκύπτει ότι κάθε γωνία του τριγώνου ΑΓΕ
είναι
0
60
συνεπώς, το τρίγωνο είναι ισόπλευρο.
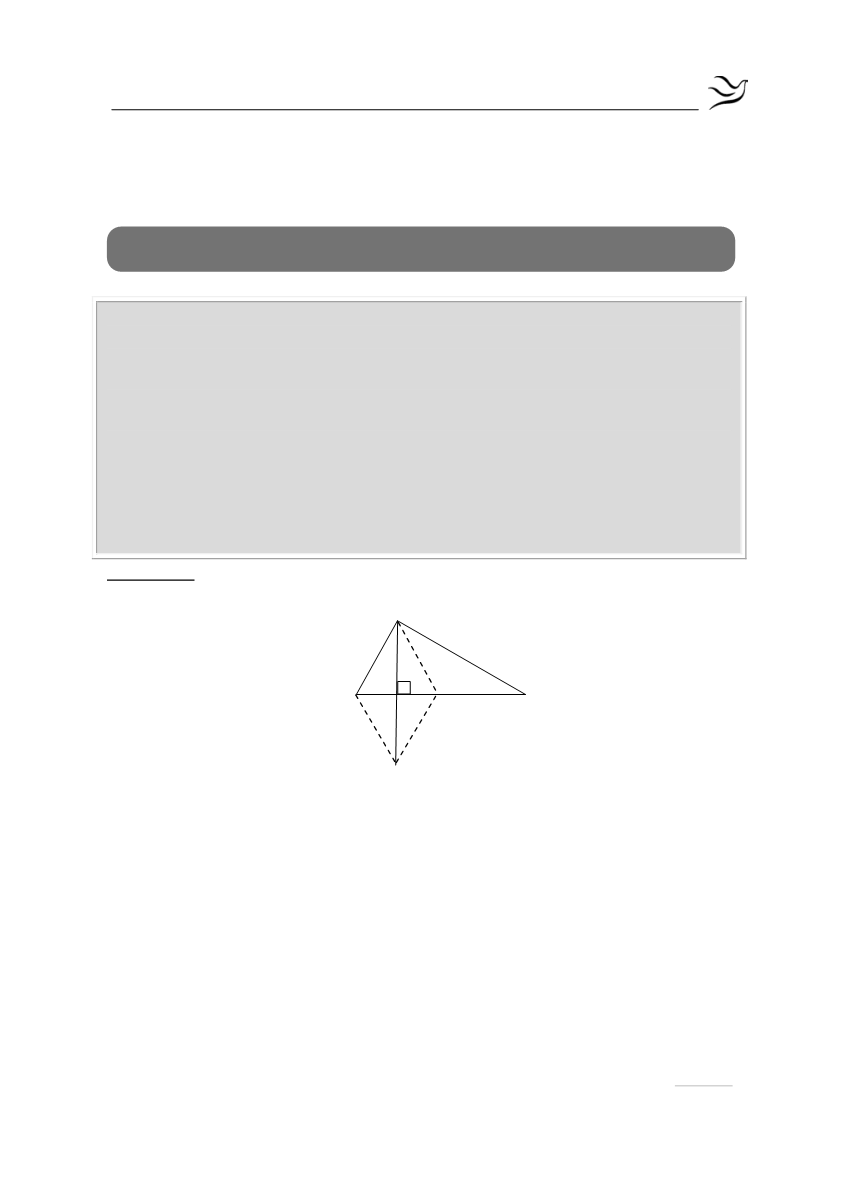
Θεωρούμε οξυγώνιο τρίγωνο ΑΒΓ με ΑΒ<ΑΓ και το ύψος του ΑΔ.
Προεκτείνουμε το ΑΔ (προς το Δ) κατά τμήμα ΔΕ=ΑΔ. Έστω Κ το συμμετρικό
του Β ως προς το Δ. Να αποδείξετε ότι:
α) το τρίγωνο ΑΒΚ είναι ισοσκελές
(Μονάδες 12)
β) το τετράπλευρο ΑΒΕΚ είναι ρόμβος.
(Μονάδες 13)
Απάντηση:
α)
Στο τρίγωνο ΑΒΚ το ΑΔ είναι ύψος και διάμεσος άρα, το τρίγωνο ΑΒΚ είναι
ισοσκελές με ΑΒ=ΑΚ (1).
β) Στο τρίγωνο ΒΕΚ το ΕΔ είναι ύψος και διάμεσος άρα, το τρίγωνο ΒΕΚ είναι
ισοσκελές με ΕΒ=ΕΚ (2). Ομοίως στο τρίγωνο ΑΒΕ το ΒΔ είναι ύψος και
διάμεσος άρα, το τρίγωνο ΑΒΕ είναι ισοσκελές με ΒΑ=ΒΕ (3). Από τις σχέσεις
(1), (2) και (3) συμπεραίνουμε ότι το τετράπλευρο ΑΒΕΚ έχει όλες του τις
πλευρές ίσες άρα, είναι παραλληλόγραμμο και ταυτόχρονα ρόμβος.
ΘΕΜΑ 3422
Α
Β
Γ
Δ
Ε
Κ
57









