Εκδόσεις ΜΠΑΧΑΡΑΚΗ – Τράπεζα Θεμάτων Γεωμετρίας Α’ Γενικού Λυκείου
Δίνεται οξυγώνιο τρίγωνο ΑΒΓ με ΑΒ<ΑΓ και γωνία
0
Γ 30
=
. Θεωρούμε το ύψος
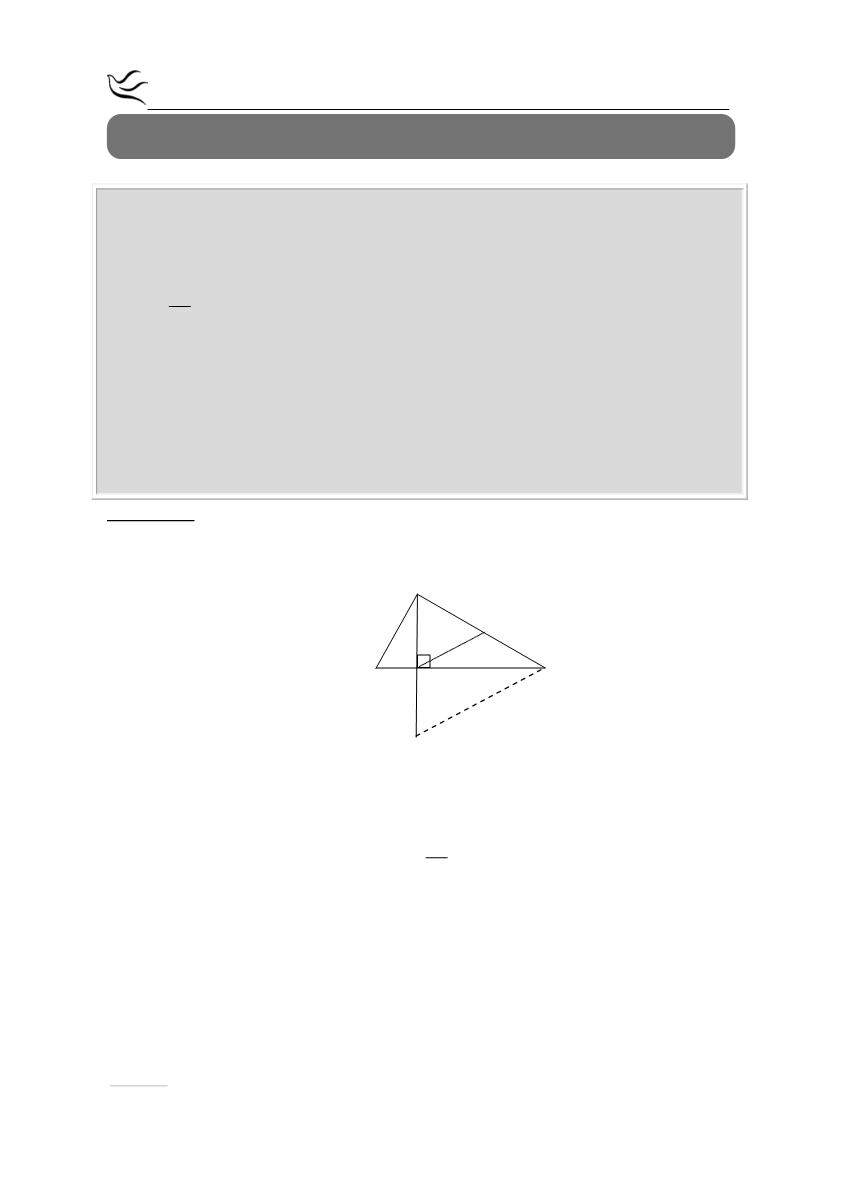
ΑΔ και το μέσο Ζ της πλευράς ΑΓ. Προεκτείνουμε το ύψος ΑΔ (προς το Δ) κατά
ίσο τμήμα ΔΕ. Να αποδείξετε ότι:
α)
ΑΓ ΔΖ
2
=
(Μονάδες 12)
β) το τρίγωνο ΑΓΕ είναι ισόπλευρο.
(Μονάδες 13)
Απάντηση:
α)
Στο ορθογώνιο τρίγωνο ΑΔΓ η
ΔΖ
είναι διάμεσος που αντιστοιχεί στην
υποτείνουσα
ΑΓ
. Άρα,
ΑΓ ΔΖ
2
=
.
β) Στο τρίγωνο ΑΓΕ το ΓΔ είναι ύψος και διάμεσος άρα, το τρίγωνο ΑΓΕ είναι
ισοσκελές με
ΑΓ ΓΕ
=
και
ΓΑΕ Ε
=
(1) ενώ επιπλέον το
ΓΔ
είναι και διχοτόμος
της γωνίας
ΑΓΕ
. Έτσι
0
0
ΑΓΕ 2 Γ 2 30 60
= ⋅ = ⋅
=
(2).
Ακόμη, στο τρίγωνο ΑΓΕ είναι
Α
Β
Γ
Δ
Ε
Ζ
30
0
ΘΕΜΑ 3419
56









