Τράπεζα Θεμάτων Γεωμετρίας Α’ Γενικού Λυκείου – Εκδόσεις ΜΠΑΧΑΡΑΚΗ
β) Στο τρίγωνο ΑΒΓ το ευθύγραμμο τμήμα ΔΕ ενώνει τα μέσα των πλευρών ΑΒ
και ΒΓ άρα, είναι ΔΕ//ΑΓ άρα και ΔΕ//ΑΖ. Ομοίως στο τρίγωνο ΑΒΓ το
ευθύγραμμο τμήμα ΖΕ ενώνει τα μέσα των πλευρών ΑΓ και ΒΓ άρα, είναι
ΖΕ//ΑΒ άρα και ΖΕ//ΑΔ. Συνεπώς, το τετράπλευρο ΔΕΖΑ έχει τις απέναντι
πλευρές του παράλληλες οπότε είναι παραλληλόγραμμο. Επομένως, ισχύει
0
BΔΕ Α 80
= =
και
0
ΕΖΓ Α 80
= =
ως εντός εκτός και επί τ’ αυτά.
γ) Επειδή το ΔΓΖΕ είναι παραλληλόγραμμο οι απέναντι γωνίες του θα είναι ίσες,
άρα, θα είναι
0
ΔΕΖ Α 80
= =
.
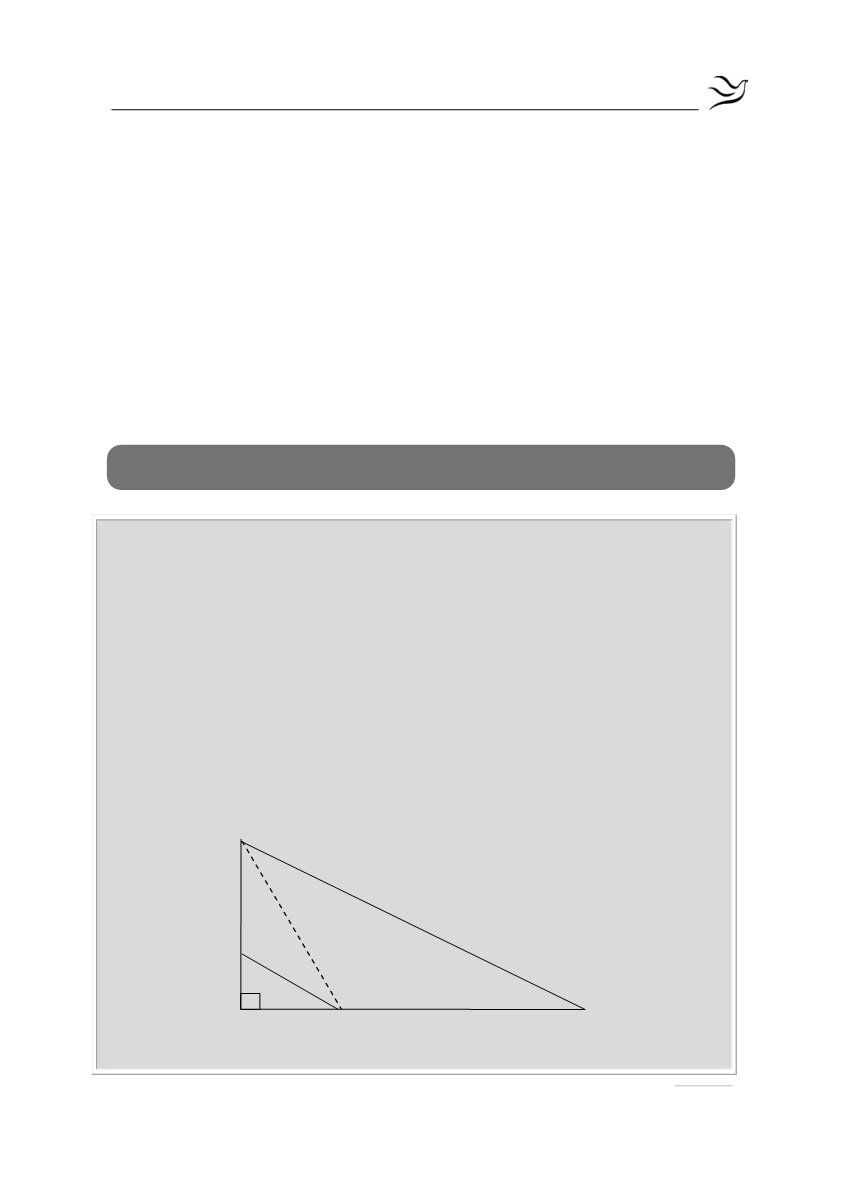
Δίνεται ορθογώνιο τρίγωνο ΑΒΓ (
0
Α 90
=
). Έστω Δ σημείο της πλευράς ΑΓ
τέτοιο, ώστε η διχοτόμος ΔΕ της γωνίας
ΑΔΒ
να είναι παράλληλη στην
πλευρά ΒΓ.
α) Να αποδείξετε ότι το τρίγωνο ΒΔΓ είναι ισοσκελές.
(Μονάδες 10)
β) Αν
0
ΑΔΒ 60
=
I. να υπολογίσετε τη γωνία
Γ
(Μονάδες 8)
II. να αποδείξετε ότι ΒΓ=2ΑΒ.
(Μονάδες 7)
Α
Β
Γ
Δ
Ε
ΘΕΜΑ 5059
61









