Τράπεζα Θεμάτων Γεωμετρίας Α’ Γενικού Λυκείου – Εκδόσεις ΜΠΑΧΑΡΑΚΗ
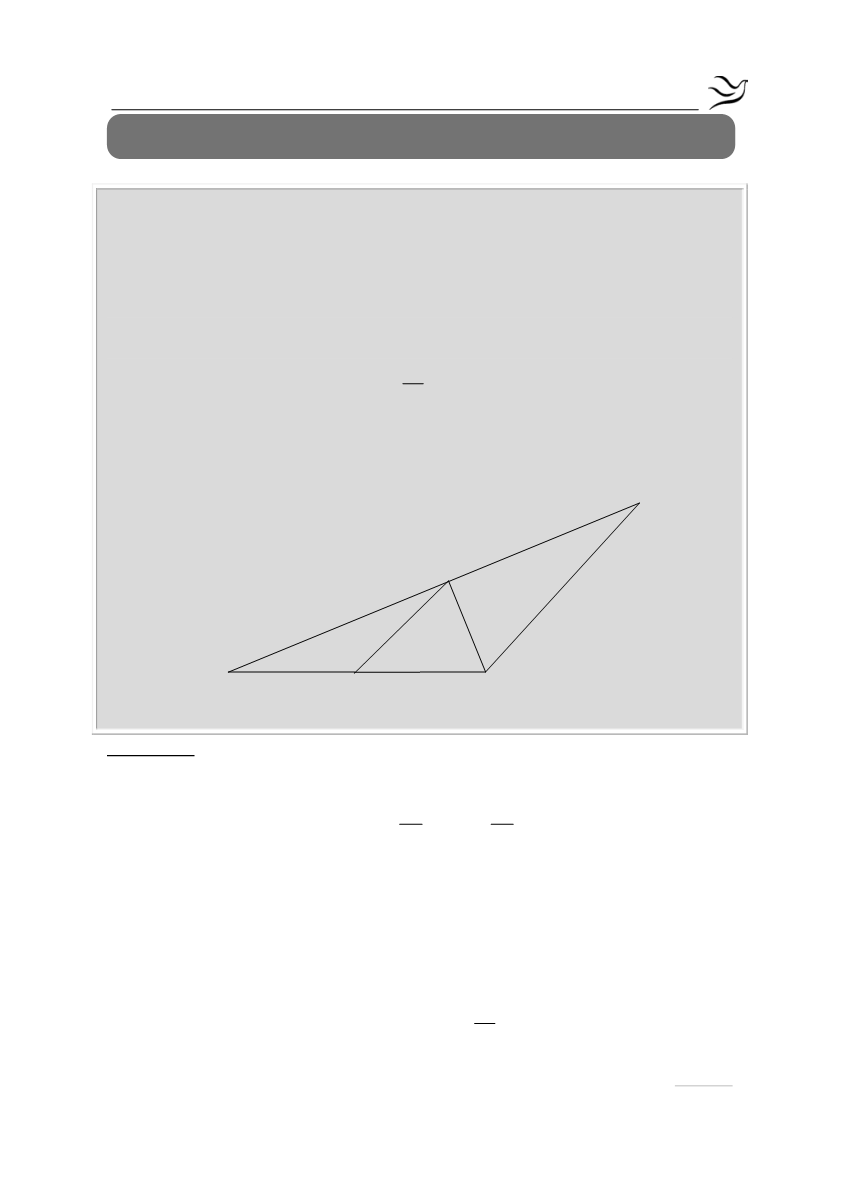
Δίνεται ισοσκελές τρίγωνο ΑΒΓ (ΑΒ = ΑΓ). Στην προέκταση της ΒΑ (προς το
μέρος της κορυφής Α) παίρνουμε σημείο Δ ώστε ΑΒ = ΑΔ και στην προέκταση
της ΔΓ (προς το μέρος της κορυφής Γ) παίρνουμε σημείο Ε ώστε ΔΓ = ΓΕ.
α) Να αποδείξετε ότι το τρίγωνο ΔΓΒ είναι ορθογώνιο.
(Μονάδες 12)
β) Να αποδείξετε ότι ΒΕ//ΑΓ και
ΒΕ ΑΓ
2
=
.
(Μονάδες 13)
Απάντηση:
α) Στο τρίγωνο ΔΓΒ, για τη διάμεσο ΓΑ που αντιστοιχεί στην ΒΔ ισχύει ότι
ΒΔ
ΑΓ ΑΒ
2
= = ⇔
ΒΔ ΑΓ
2
=
.
Άρα, το τρίγωνο ΔΓΒ είναι ορθογώνιο με
0
ΔΓΒ 90
=
.
β) Από την υπόθεση έχουμε ότι το σημείο Α είναι το μέσο του ΒΔ και ότι το
σημείο Γ είναι το μέσο του ΔΕ. Συνεπώς, στο τρίγωνο ΒΔΕ το τμήμα ΑΓ ενώνει
τα μέσα των πλευρών ΔΒ και ΔΕ, οπότε
ΒΕ // ΑΓ και
ΒΕ ΑΓ
2
=
.
Δ
Β
Γ
A
Ε
/
/
//
//
ΘΕΜΑ 2852
55









