Εκδόσεις ΜΠΑΧΑΡΑΚΗ – Τράπεζα Θεμάτων Γεωμετρίας Α’ Γενικού Λυκείου
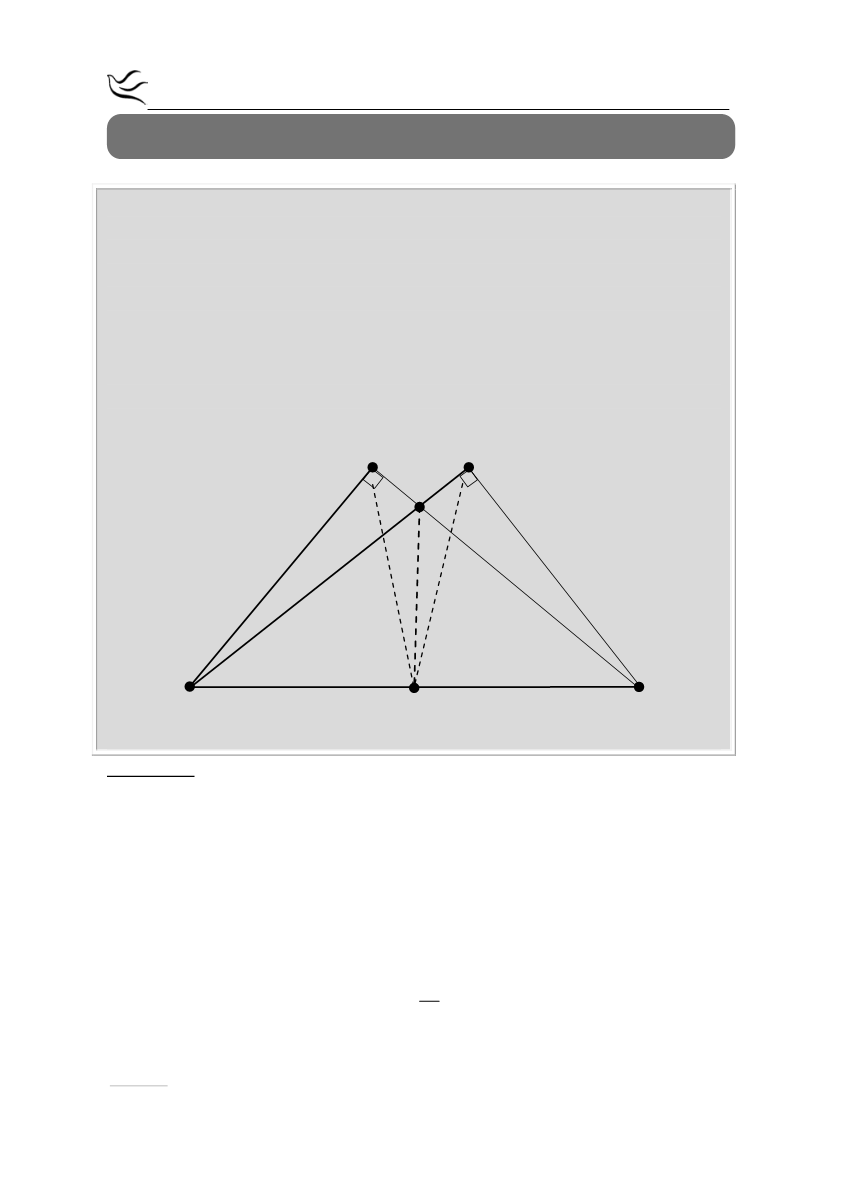
Έστω ισοσκελές τρίγωνο
=
ΑΒΓ (ΑΒ ΑΓ)
. Στις προεκτάσεις των πλευρών ΑΒ και
ΑΓ προς το Α φέρουμε τμήματα ΒΔ και ΓΕ κάθετα στις ΑΓ και ΑΒ αντίστοιχα.
α) Να αποδείξετε ότι ΒΔ = ΓΕ.
(Μονάδες 10)
β) Αν Μ το μέσο της ΒΓ τότε:
i. να αποδείξετε ότι ΜΔ = ΜΕ
(Μονάδες 8)
ii. να αποδείξετε ότι η ΑΜ διχοτομεί τη γωνία
ΔΜΕ
.
(Μονάδες 7)
Απάντηση:
α) Τα τρίγωνα ΓΔΒ και ΒΕΓ είναι ίσα γιατί
•
0
ΓΔΒ ΓΕΒ 90
= =
•
ΓΒ κοινή
•
Β Γ
=
ως προσκείμενες στη βάση του ισοσκελούς τριγώνου ΑΒΓ.
Άρα, ΒΔ=ΓΕ.
β) i) Στο ορθογώνιο ΒΔΓ η ΔΜ είναι διάμεσος που αντιστοιχεί στην υποτείνουσα
ΒΓ άρα,
ΒΓ
ΔΜ
2
=
(1).
Ομοίως, η ΕΜ είναι διάμεσος που αντιστοιχεί στην υποτείνουσα ΒΓ άρα,
Γ
Μ
Β
Α
Ε
Δ
ΘΕΜΑ 5638
78









