Τράπεζα Θεμάτων Γεωμετρίας Α’ Γενικού Λυκείου – Εκδόσεις ΜΠΑΧΑΡΑΚΗ
ΒΓ
ΕΜ
2
=
(2).
Από (1) και (2) συμπεραίνουμε ότι ΔΜ = ΕΜ.
ii) Από α) ερώτημα προκύπτει ότι ΒΕ=ΓΔ οπότε ΔΑ=ΕΑ ως διαφορές ίσων
τμημάτων.
Τα τρίγωνα ΔΑΜ και ΕΑΜ είναι ίσα γιατί
•
ΑΜ κοινή
•
ΔΜ=ΕΜ από i) ερώτημα
•
ΔΑ=ΕΑ.
Άρα,
ΔΜΑ ΑΜΕ
=
δηλαδή η ΑΜ διχοτομεί τη γωνία
ΔΜΕ
.
Απάντηση:
α)
Οι γωνίες
Β
και
ΓΑΔ
είναι ίσες ως οξείες γωνίες με πλευρές κάθετες.
(
ΒΑ ΑΓ
⊥
και
ΒΓ ΑΔ
⊥
).
β) Η ΑΜ είναι διάμεσος που αντιστοιχεί στην υποτείνουσα ΒΓ του ορθογωνίου
τριγώνου ΑΒΓ. Συνεπώς, ΑΜ=ΜΓ άρα και
ΜΑΓ Γ
=
(1).
Όμως η γωνία
ΑΜΔ
είναι εξωτερική του τριγώνου ΑΜΓ οπότε θα ισχύει
( )
1
ΑΜΔ ΜΑΓ Γ
= + ⇔
ΑΜΔ Γ Γ
= + ⇔
ΑΜΔ 2Γ
=
.
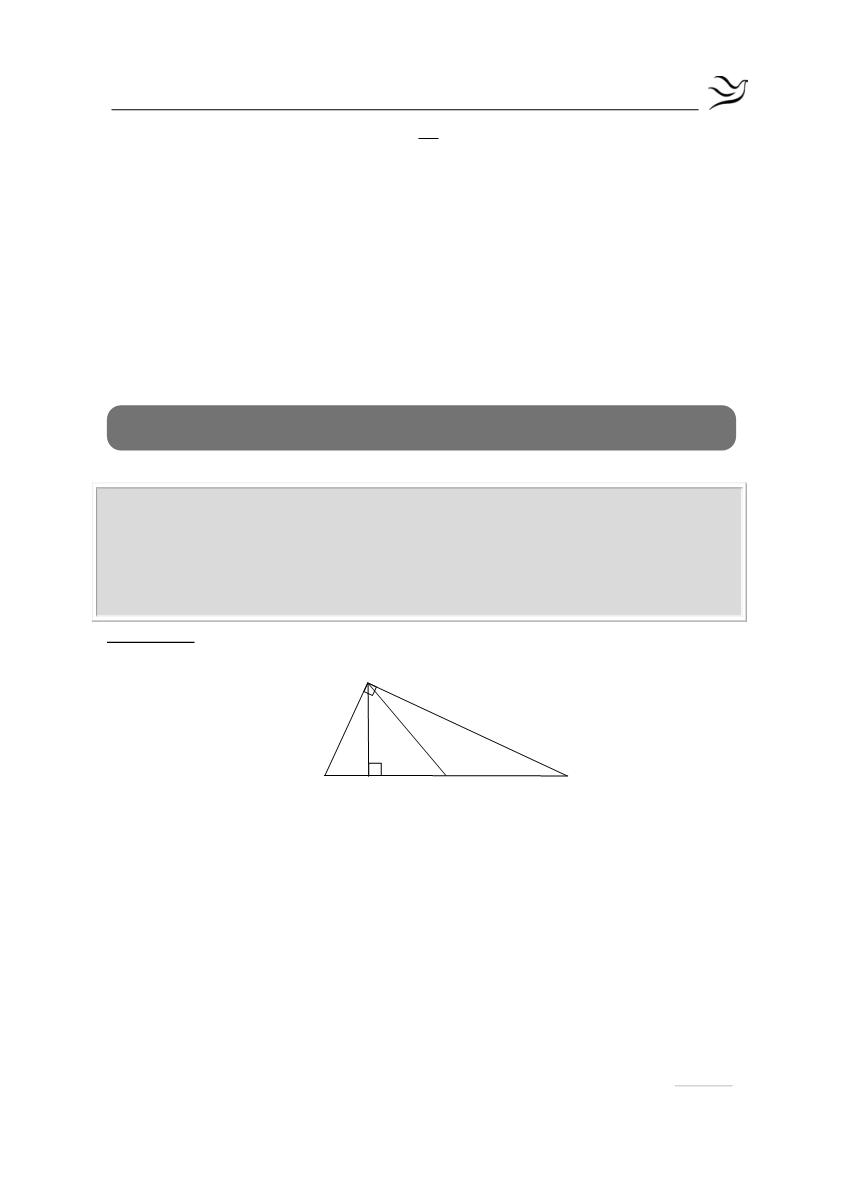
Σε ορθογώνιο τρίγωνο ΑΒΓ με
0
Α 90
=
και
Β Γ
>
φέρουμε το ύψος του ΑΔ και
την διάμεσο ΑΜ στην πλευρά ΒΓ. Να αποδείξετε ότι:
α) οι γωνίες
Β
και
ΓΑΔ
είναι ίσες (Μονάδες 12)
β)
ΑΜΔ 2Γ
=
. (Μονάδες 13)
ΘΕΜΑ 6580
Α
Β
Μ
Δ
Γ
79









