Γεωμετρία A' Λυκείου (Τράπεζα Θεμάτων)

86 / 226

Τράπεζα Θεμάτων Γεωμετρίας Α’ Γενικού Λυκείου – Εκδόσεις ΜΠΑΧΑΡΑΚΗ
Απάντηση:
α) Η γωνία 
ΒΓΔ είναι εγγεγραμμένη, η οποία βαίνει στο ίδιο τόξο με την
επίκεντρη γωνία 
ΒΟΔ οπότε θα είναι
  ο
ο ΒΟΔ 120
ΒΓΔ 60
2 2
= = = .
β) Η γωνία 
ΒΓΔ είναι εξωτερική γωνία στο τρίγωνο ΒΓΜ οπότε θα είναι
   ο ο ο ο ο ΒΓΔ ΒΜΓ ΓΒΜ 60 ω 15 ω 60 15 ω 45= + ⇔ = + ⇔ = − ⇔ = .
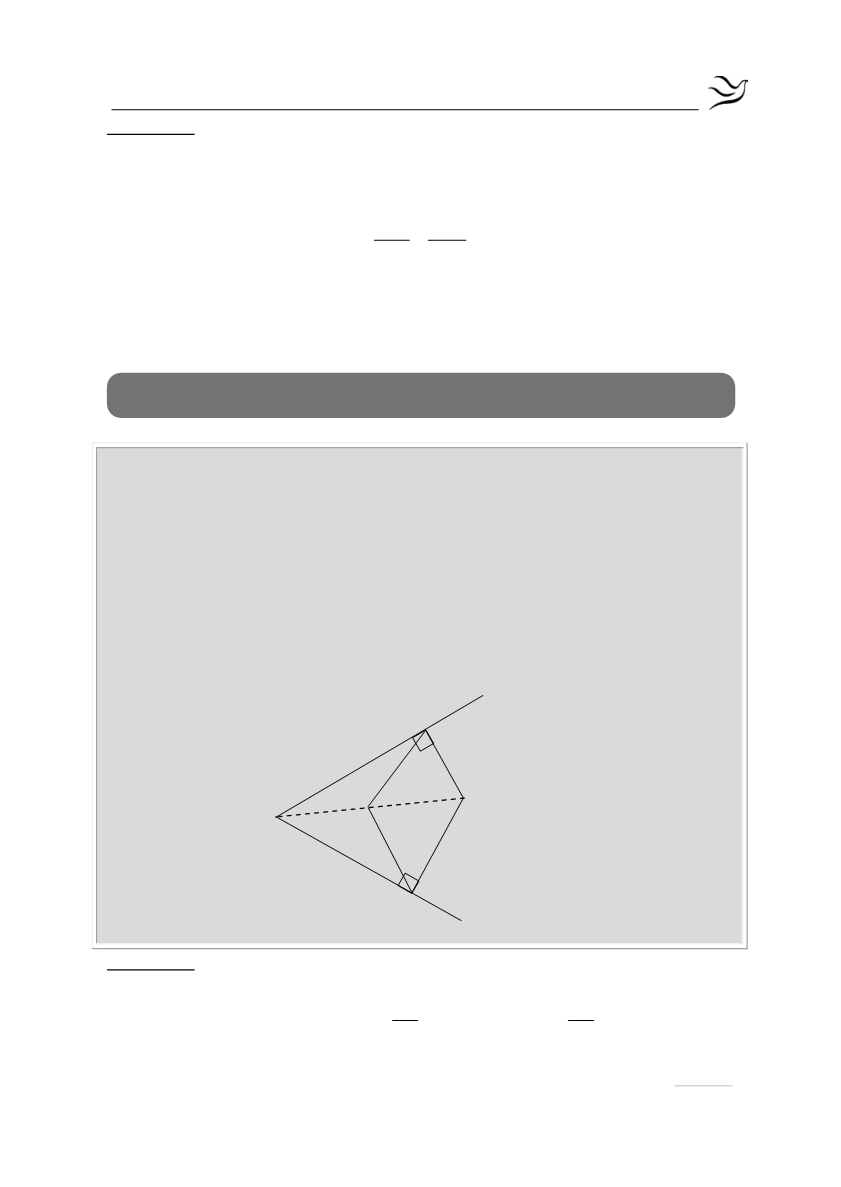
Δίνεται γωνία 
xΟy και σημείο Α στο εσωτερικό της. Από το Α φέρνουμε τις
κάθετες ΑΒ, ΑΓ προς τις πλευρές Οx, Oy της γωνίας αντίστοιχα, και
ονομάζουμε Μ το μέσο του ΟΑ. Να αποδείξετε ότι:
α) το τρίγωνο ΒΜΓ είναι ισοσκελές
(Μονάδες 10)
β)  
ΒΜΓ 2 xΟy= ⋅
(Μονάδες 15)
Απάντηση:
α) Στο ορθογώνιο τρίγωνο ΟΒΑ η ΒΜ είναι διάμεσος που αντιστοιχεί στην
υποτείνουσα ΟΑ άρα, θα είναι ΟΑ ΒΜ
2
= (1). Ομοίως ΟΑ ΓΜ
2
= (2).
ΘΕΜΑ 5033
Α
Β
Γ
Μ
y
O
x
85