Εκδόσεις ΜΠΑΧΑΡΑΚΗ – Τράπεζα Θεμάτων Γεωμετρίας Α’ Γενικού Λυκείου
Απάντηση:
α)
Τα τρίγωνα ΔΑΗ και ΓΒΘ είναι ίσα γιατί
•
= =
0
AHΔ ΒΘΓ 90
•
=
AΔH ΒΓΘ
ως προσκείμενες σε βάση ισοσκελούς τραπεζίου
•
ΔΑ=ΒΓ αφού το τραπέζιο είναι ισοσκελές.
Άρα, ΔΗ = ΘΓ.
β) Έστω Μ το μέσο της ΑΔ και Ν το μέσο της ΒΓ. Τότε για τη διάμεσο ΜΝ του
τραπεζίου θα είναι
+
=
⇔
ΑΒ ΔΓ
ΜΝ
2
+
=
⇔
8 12
ΜΝ
2
= ⇔
20 ΜΝ
2
=
ΜΝ 10
.
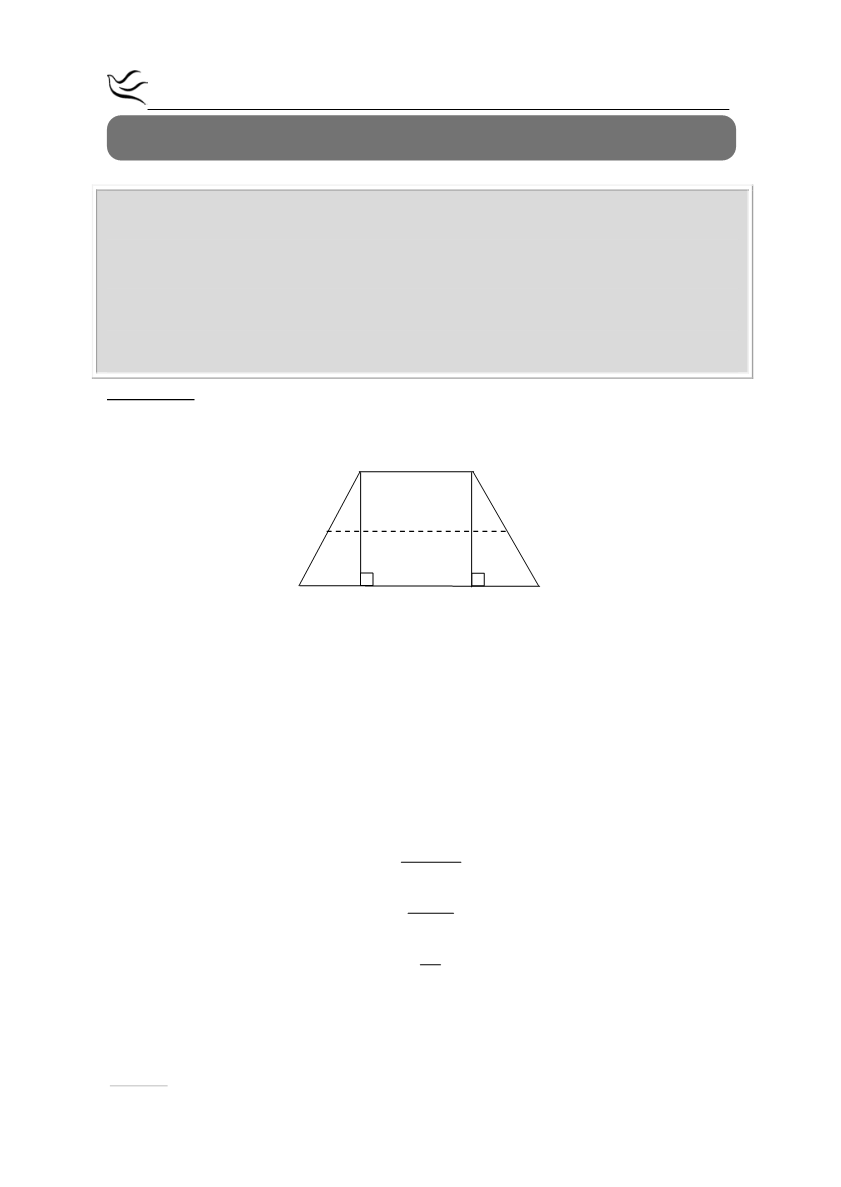
Δίνεται ισοσκελές τραπέζιο ΑΒΓΔ (ΑΒ//ΓΔ ) με ΑΒ=8 και ΔΓ=12. Αν ΑΗ και ΒΘ
τα ύψη του τραπεζίου
α) να αποδείξετε ότι ΔΗ = ΘΓ
(Μονάδες 12)
β) να υπολογίσετε τη διάμεσο του τραπεζίου.
(Μονάδες 13)
Α
Β
Γ
Δ
Θ
Η
Μ
Ν
ΘΕΜΑ 6585
80









