Εκδόσεις ΜΠΑΧΑΡΑΚΗ – Τράπεζα Θεμάτων Γεωμετρίας Α’ Γενικού Λυκείου
Απάντηση:
α) Από την εκφώνηση είναι ΒΓ=2ΒΕ (1). Ακόμη, επειδή ΑΜ διάμεσος θα είναι
και ΒΓ=2ΒΜ (2). Από τις σχέσεις (1) και (2) προκύπτει ότι ΒΕ=ΒΜ δηλαδή ότι το
τρίγωνο ΒΕΜ είναι ισοσκελές με
ΒΕΜ ΒΜΕ
=
. Άρα, θα είναι και
ΑΕΒ ΕΜΓ
=
ως παραπληρωματικές ίσων γωνιών.
β) Τα τρίγωνα ΑΕΒ και ΕΜΓ είναι ίσα γιατί
•
ΑΕ=ΕΜ
•
ΒΕ=ΜΓ (=ΒΜ) και
•
ΑΕΒ ΕΜΓ
=
.
Άρα, ΑΒ = ΕΓ.
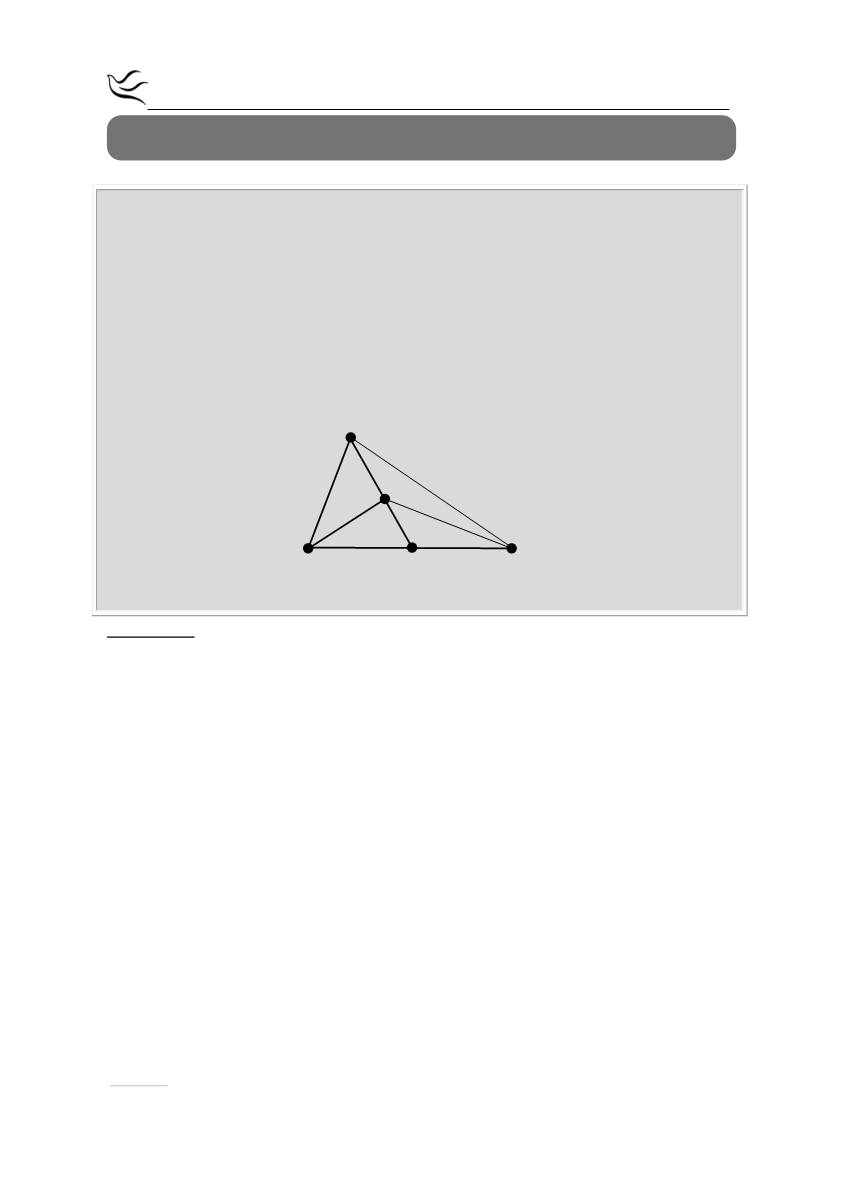
Δίνεται τρίγωνο ΑΒΓ και Ε το μέσο της διαμέσου του ΑΜ. Αν ΒΓ=2ΒΕ να
αποδείξετε ότι:
α)
ΑΕΒ ΕΜΓ
=
(Μονάδες 12)
β) ΑΒ = ΕΓ.
(Μονάδες 13)
Α
Β
Μ
Γ
Ε
ΘΕΜΑ 5597
22









