Τράπεζα Θεμάτων Γεωμετρίας Α’ Γενικού Λυκείου – Εκδόσεις ΜΠΑΧΑΡΑΚΗ
Απάντηση:
α) Επειδή το σημείο Δ ανήκει στη διχοτόμο της γωνίας Β θα ισαπέχει από τις
πλευρές της άρα, θα ισχύει ΔΑ=ΔΕ.
β) Σύμφωνα με το α) ερώτημα αρκεί να δείξουμε ότι ΔΕ < ΔΓ, που ισχύει αφού
στο ορθογώνιο τρίγωνο ΔΕΓ η ΔΓ είναι η υποτείνουσα.
γ) Σύμφωνα με την εκφώνηση στο τρίγωνο ΑΒΓ είναι
<
Γ Β
άρα και οι απέναντι
πλευρές του θα είναι ομοιοτρόπως άνισες συνεπώς, ΑΓ > ΑΒ.
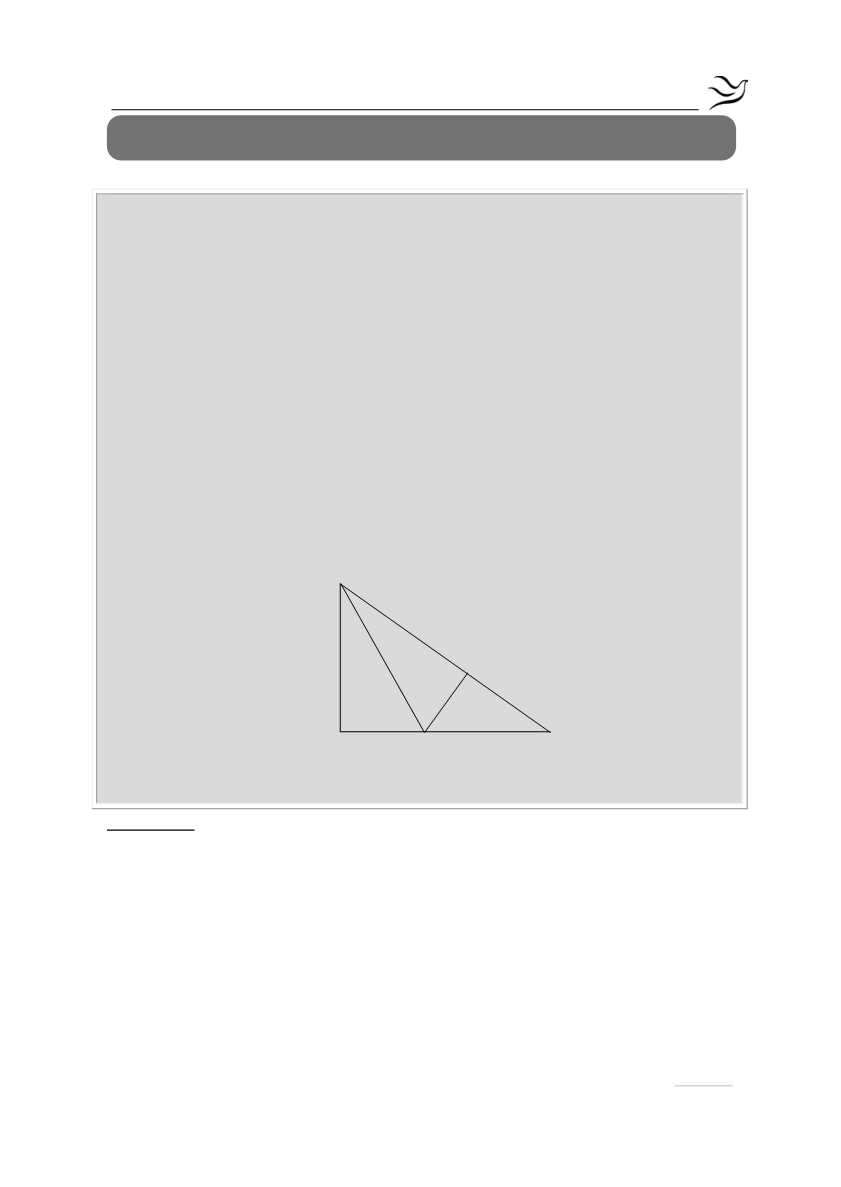
Στο παρακάτω σχήμα το τρίγωνο ΑΒΓ είναι ορθογώνιο με ορθή τη γωνία
Α
. Η
ΒΔ είναι διχοτόμος της γωνίας
Β
, η ΔΕ είναι κάθετη στη ΒΓ και η γωνία
Γ
είναι
μικρότερη της γωνίας
Β
. Να αποδείξετε ότι:
α) ΑΔ=ΔΕ
(Μονάδες 8)
β) ΑΔ<ΔΓ
(Μονάδες 9)
γ) ΑΓ>ΑΒ.
(Μονάδες 8)
ΘΕΜΑ 5580
Α
Β
Γ
Δ
Ε
21









