Γεωμετρία A' Λυκείου (Τράπεζα Θεμάτων)

Εκδόσεις ΜΠΑΧΑΡΑΚΗ – Τράπεζα Θεμάτων Γεωμετρίας Α’ Γενικού Λυκείου

Απάντηση:

α) Για να αποδείξουμε ότι οι χορδές ΔΓ και ΖΕ του κύκλου (Ο, R) είναι ίσες

αρκεί να είναι ίσα τα αποστήματά τους. Αυτό όμως ισχύει γιατί τα αποστήματά

τους είναι τα ΟΑ και ΟΒ, τα οποία είναι ίσα ως ακτίνες του κύκλου (Ο, ρ).

β) Είναι ΚΑ=ΚΒ (1) ως εφαπτόμενα τμήματα. Επειδή όμως το απόστημα μιας

χορδής διέρχεται από το μέσο της θα είναι και ΑΓ=ΒΕ (2) ως μισά των ίσων

χορδών ΔΓ και ΖΕ.

Από τις σχέσεις (1) και (2) προκύπτει ότι ΚΓ=ΚΕ ως διαφορές ίσων τμημάτων

οπότε, το τρίγωνο ΚΕΓ είναι ισοσκελές.

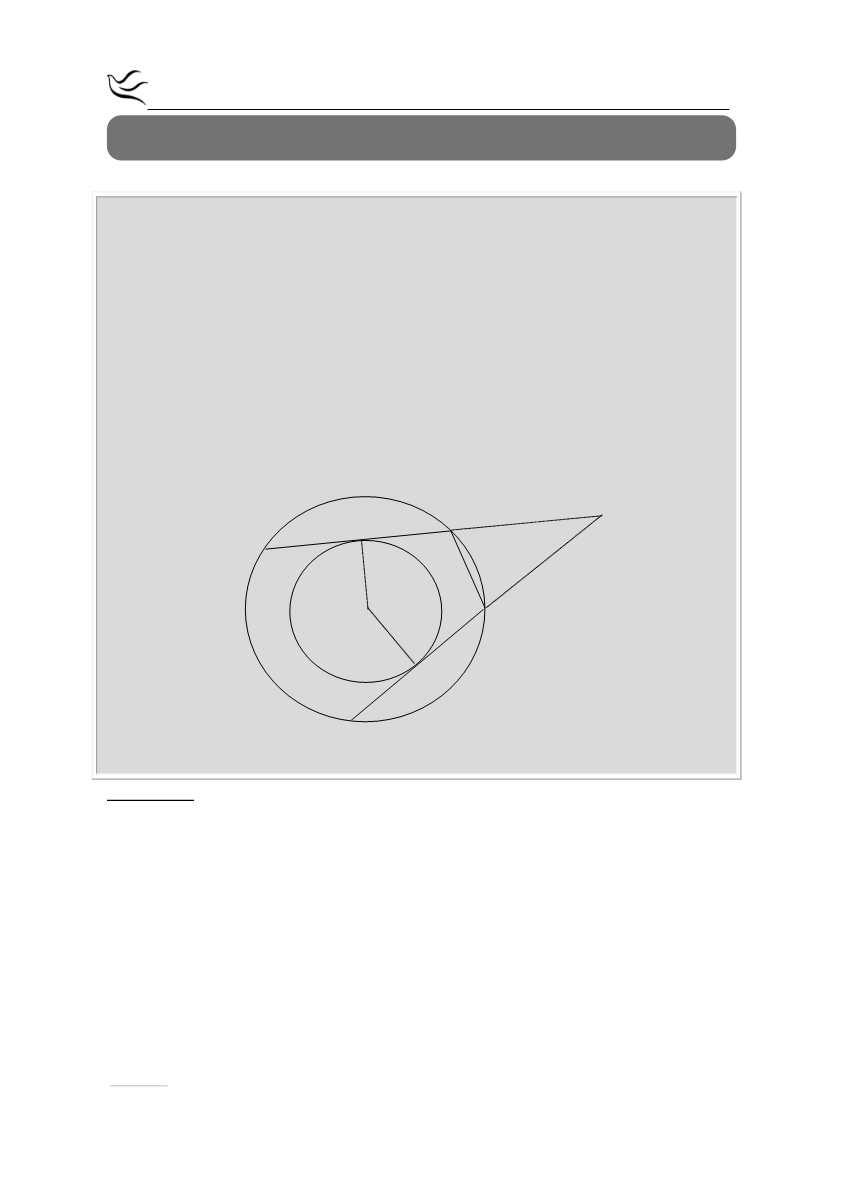
Δίνονται δύο ομόκεντροι κύκλοι με κέντρο Ο και ακτίνες ρ και R (ρ < R). Οι

χορδές ΔΓ και ΖΕ του κύκλου (Ο, R) εφάπτονται του κύκλου (Ο, ρ) στα σημεία Α

και Β αντίστοιχα.

α) Να αποδείξετε ότι ΔΓ=ΖΕ.

(Μονάδες 12)

β) Αν οι ΔΓ και ΖΕ προεκτεινόμενες τέμνονται στο σημείο Κ, να αποδείξετε ότι

το τρίγωνο ΚΕΓ είναι ισοσκελές.

(Μονάδες 13)

•

ΘΕΜΑ 5613