Τράπεζα Θεμάτων Γεωμετρίας Α’ Γενικού Λυκείου – Εκδόσεις ΜΠΑΧΑΡΑΚΗ
δ) Τα τρίγωνα ΑΒΖ και ΓΖΛ είναι ίσα γιατί
•
= =
0
Α Λ 90
•
=
ΒΖΑ ΓΖΛ
ως κατακορυφήν
•
ΓΖ=ΖΒ.
Άρα, θα είναι και ΖΑ=ΖΛ (7).
Προσθέτοντας τέλος τις σχέσεις (5) και (7) κατά μέλη προκύπτει ότι
+ = + ⇔
ΓΖ ΖΑ ΒΖ ΖΛ
=
ΑΓ ΒΛ
.
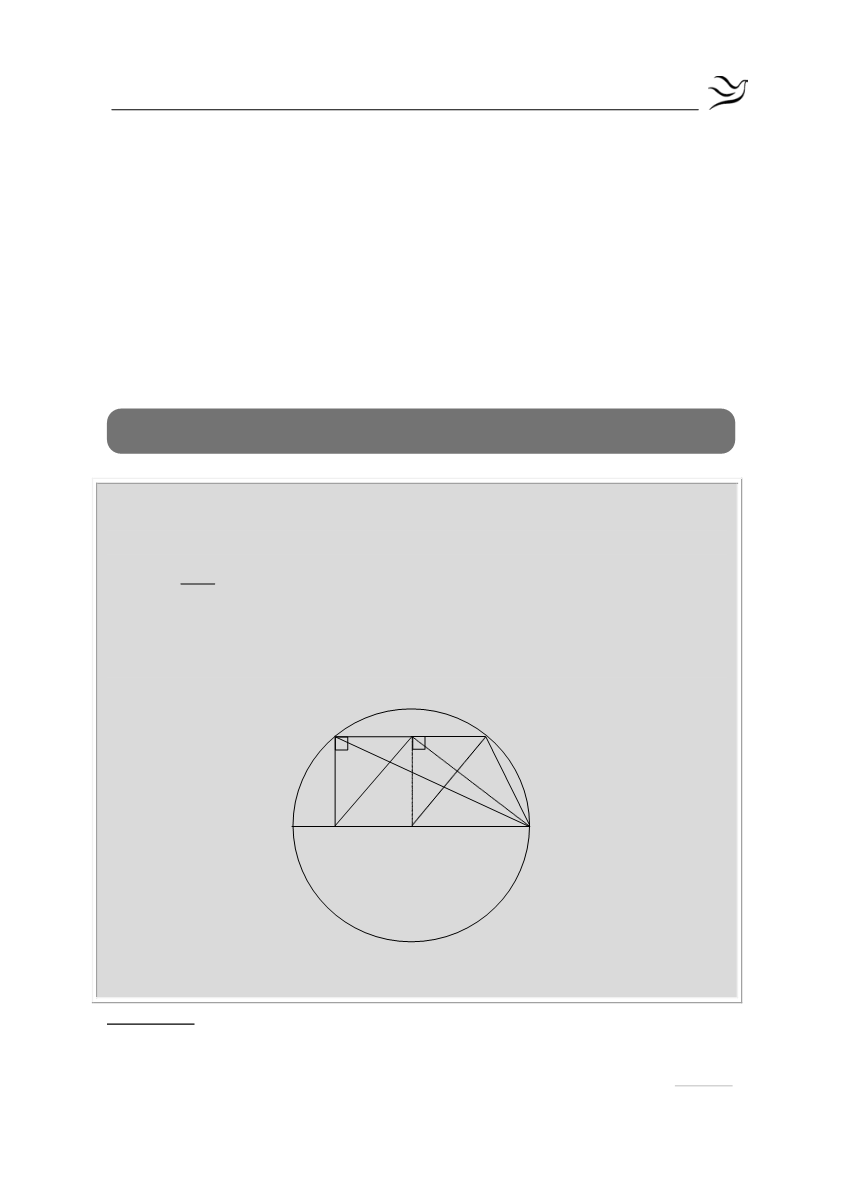
Έστω κύκλος με κέντρο Ο και διάμετρο ΑΒ. Φέρνουμε χορδή ΓΔ // ΑΒ με Κ το
μέσο της. Από το Δ φέρνουμε το τμήμα ΔΕ κάθετο στη ΔΓ. Να αποδείξετε ότι:
α) το τετράπλευρο ΚΓΟΕ είναι παραλληλόγραμμο (Μονάδες 8)
β)
=
ΔΟΓ
ΔΕΚ
2
(Μονάδες 12)
γ) ΚΕ< ΚΒ . (Μονάδες 5)
Απάντηση:
α)
Δ
Κ
Γ
Ε
Α
Β
Ο
ΘΕΜΑ 4814
217









