Τράπεζα Θεμάτων Γεωμετρίας Α’ Γενικού Λυκείου – Εκδόσεις ΜΠΑΧΑΡΑΚΗ
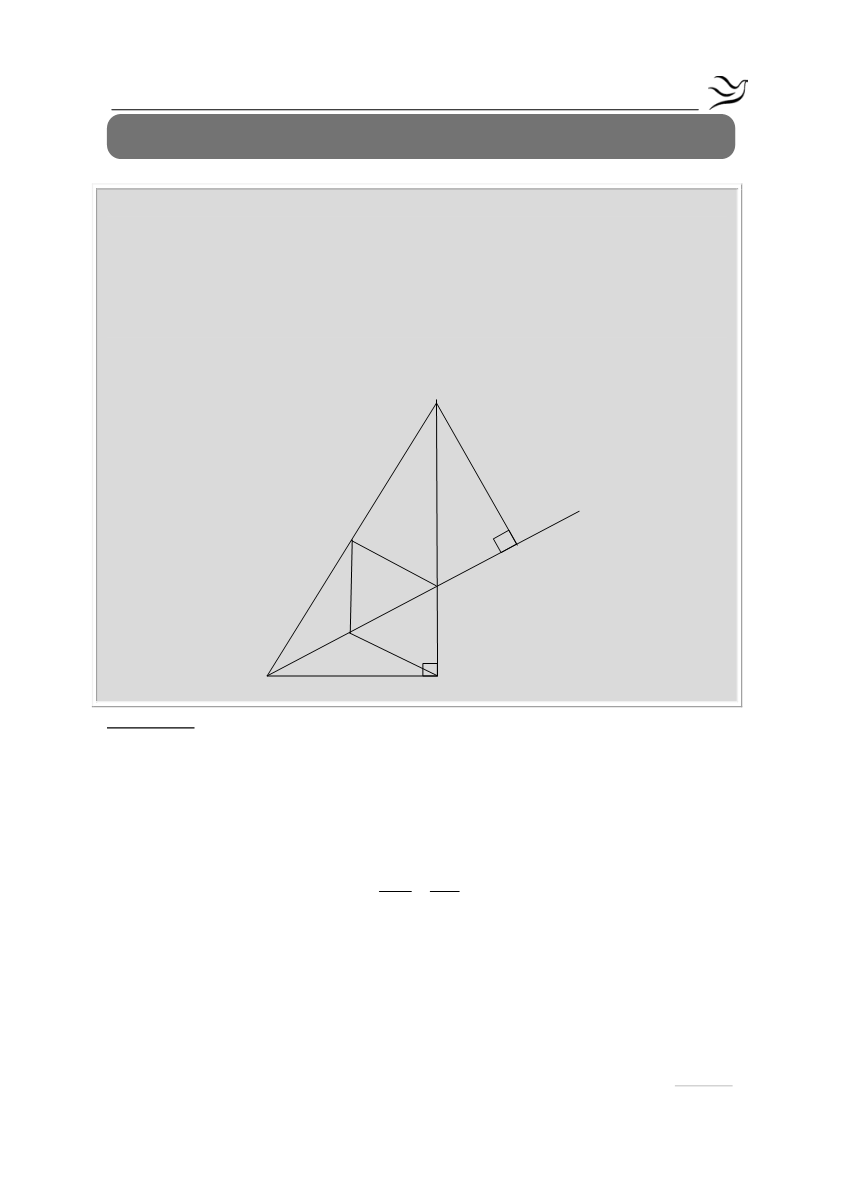
Έστω ορθογώνιο τρίγωνο ΑΒΓ με
=
0
Α 90
και
=
0
Β 60
. Η διχοτόμος της γωνίας
Β
τέμνει την ΑΓ στο Ζ. Τα σημεία Μ και Κ είναι τα μέσα των ΒΖ και ΒΓ
αντίστοιχα. Αν το τμήμα ΓΛ είναι κάθετο στη διχοτόμο Βδ να αποδείξετε ότι:
α) το τρίγωνο ΒΖΓ είναι ισοσκελές (Μονάδες 6)
β) το τετράπλευρο ΑΜΚΖ είναι ρόμβος (Μονάδες 6)
γ) ΓΖ=2ΖΑ (Μονάδες 7)
δ) ΒΛ=ΑΓ. (Μονάδες 6)
Απάντηση:
α) Στο ορθογώνιο τρίγωνο ΑΒΓ είναι
+ = ⇔
0
ΑΒΓ ΒΓΑ 90
+ = ⇔
0
0
60 ΒΓΑ 90
=
0
ΒΓΑ 30
.
Ακόμη, η ΒΖ είναι διχοτόμος της γωνίας
ΑΒΓ
άρα,
= = =
0
0
ΑΒΓ 60
ΖΒΓ
30
2 2
.
Συνεπώς, είναι
=
ΒΓΑ ΖΒΓ
δηλαδή το τρίγωνο ΒΖΓ είναι ισοσκελές.
β) Στο ισοσκελές τρίγωνο ΒΖΓ η ΖΚ είναι διάμεσος και ύψος. Έτσι στο ορθογώνιο
τρίγωνο ΒΚΖ η ΚΜ είναι διάμεσος που αντιστοιχεί στην υποτείνουσα ΒΖ οπότε
θα ισούται με το μισό της δηλαδή θα είναι
Β
Λ
Γ
A
Ζ
Μ
Κ
δ
ΘΕΜΑ 4802
215









