Εκδόσεις ΜΠΑΧΑΡΑΚΗ – Τράπεζα Θεμάτων Γεωμετρίας Α’ Γενικού Λυκείου
Το ΟΚ είναι το απόστημα της χορδής ΓΔ άρα είναι
⊥
ΟΚ ΓΔ
. Ακόμη, είναι και
⊥
ΕΔ ΓΔ
άρα, προκύπτει ότι
ΟΚ//ΕΔ (1).
Ακόμη, αφού ΔΓ//ΑΒ θα είναι
ΔΚ//ΕΟ (2).
Από τις σχέσεις (1) και (2) συμπεραίνουμε ότι το τετράπλευρο ΔΚΟΕ έχει τις
απέναντι πλευρές του παράλληλες άρα, είναι παραλληλόγραμμο και επειδή
=
0
ΕΔΚ 90
είναι και ορθογώνιο. Άρα, θα είναι
=
ΟΕ // ΔΚ
άρα και
=
ΟΕ // ΚΓ
.
Συνεπώς, και το τετράπλευρο ΚΓΟΕ έχει δύο απέναντι πλευρές του ίσες και
παράλληλες άρα, είναι παραλληλόγραμμο.
β) Τα τρίγωνα ΔΕΚ και ΚΟΔ είναι ίσα γιατί
•
= =
0
ΕΔΚ ΟΚΔ 90
•
ΚΔ κοινή
•
ΔΕ=ΚΟ ως απέναντι πλευρές του ορθογωνίου ΔΚΟΕ.
Άρα, θα είναι και
=
ΔΕΚ ΔΟΚ
(3).
Όμως στο τρίγωνο ΔΟΓ, που είναι ισοσκελές γιατί ΟΔ=ΟΓ, το ύψος ΟΚ που
αντιστοιχεί στη βάση ΔΓ είναι και διχοτόμος οπότε
=
ΔΟΓ
ΔΟΚ
2
(4).
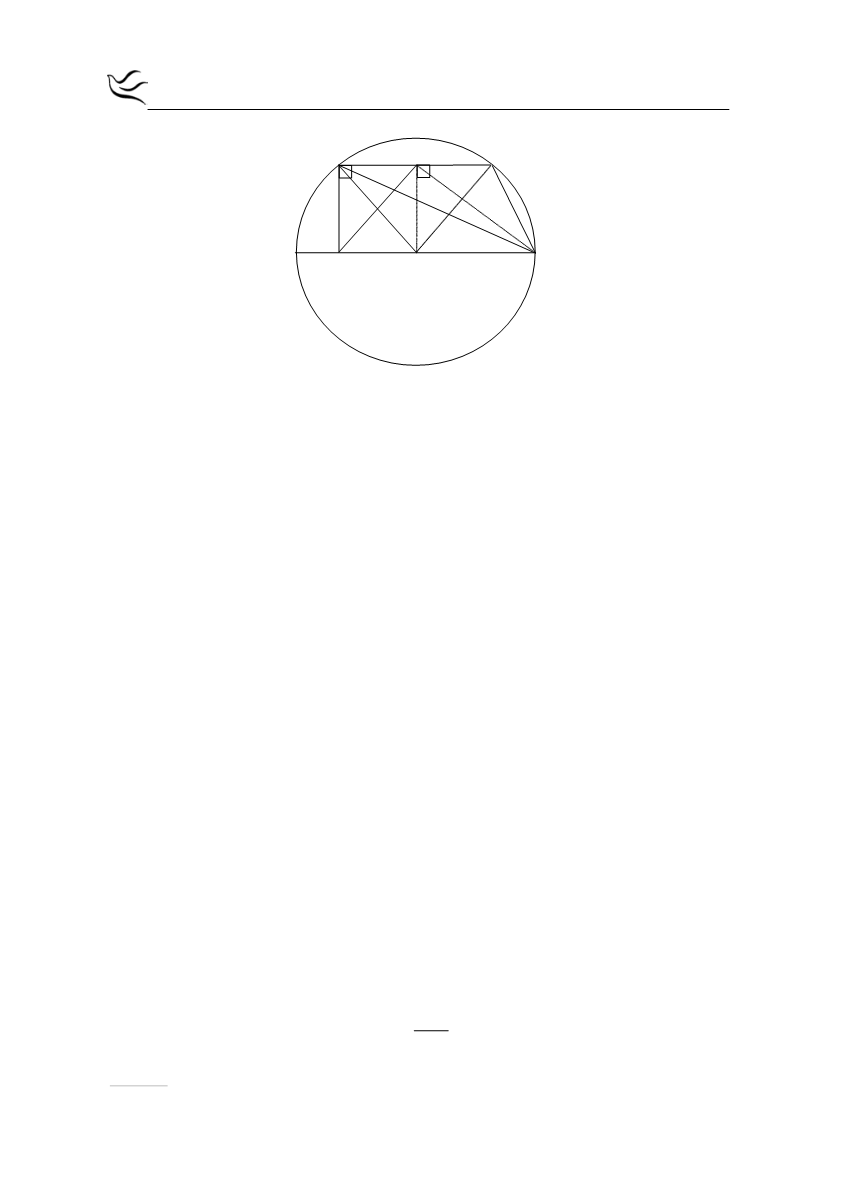
Α
Δ
Κ
Γ
Ε
Β
Ο
218









