Γεωμετρία A' Λυκείου (Τράπεζα Θεμάτων)

Τράπεζα Θεμάτων Γεωμετρίας Α’ Γενικού Λυκείου – Εκδόσεις ΜΠΑΧΑΡΑΚΗ

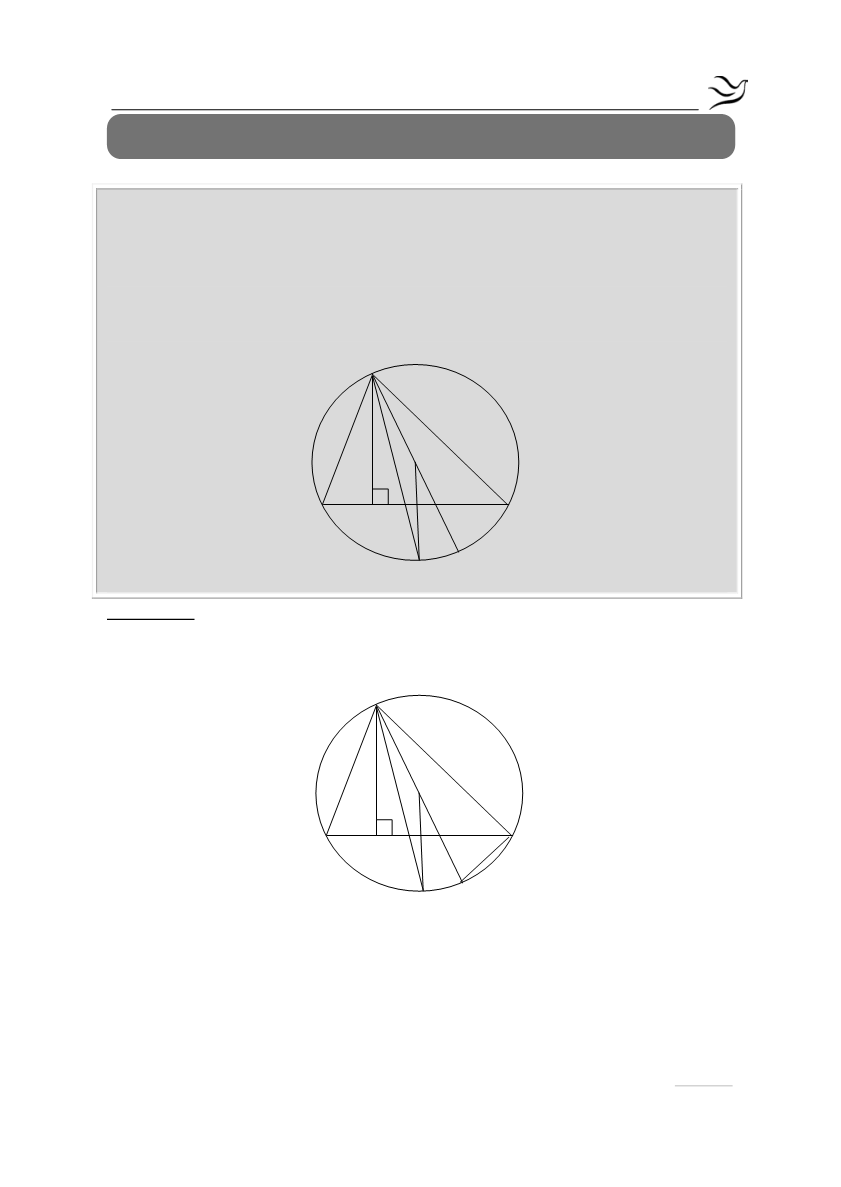
Δίνεται τρίγωνο ΑΒΓ με ΑΒ<ΑΓ, εγγεγραμμένο σε κύκλο με κέντρο Ο.

Θεωρούμε το μέσο Μ του κυρτογώνιου τόξου ΒΓ και το ύψος ΑΔ του τριγώνου

ΑΒΓ. Να αποδείξετε ότι:

α) η ΑΜ είναι διχοτόμος της γωνίας



ΔΑΟ

(Μονάδες 8)

β)

 

ΟΑΓ ΔΑΒ

(Μονάδες 9)

γ)



= −

 

ΔΑΟ Β Γ

. (Μονάδες 8)

Απάντηση:

α) Έστω Κ το σημείο τομής των ΟΜ και ΒΓ.

Επειδή το Μ είναι το μέσο του τόξου



ΒΓ

η ΟΚ θα είναι το απόστημα της χορδής

ΒΓ. Άρα, θα είναι

⊥

ΟΚ ΒΓ

. Ακόμη, είναι

⊥

ΑΔ ΒΓ

άρα, προκύπτει ότι ΟΚ//ΑΔ.

Επομένως, θα είναι

•

ΘΕΜΑ 5910

221