Τράπεζα Θεμάτων Γεωμετρίας Α’ Γενικού Λυκείου – Εκδόσεις ΜΠΑΧΑΡΑΚΗ
γ) Είναι
⊥
ΛΝ ΒΓ
(1) επειδή οι διαγώνιοι του ρόμβου τέμνονται κάθετα.
Στο τρίγωνο ΑΒΓ είναι
•
Λ μέσο της ΑΒ
•
Μ μέσο της ΑΓ.
Άρα, ΛΜ//ΒΓ (2).
Από τις σχέσεις (1) και (2) συμπεραίνουμε ότι
⊥
ΛΜ ΛΝ
.
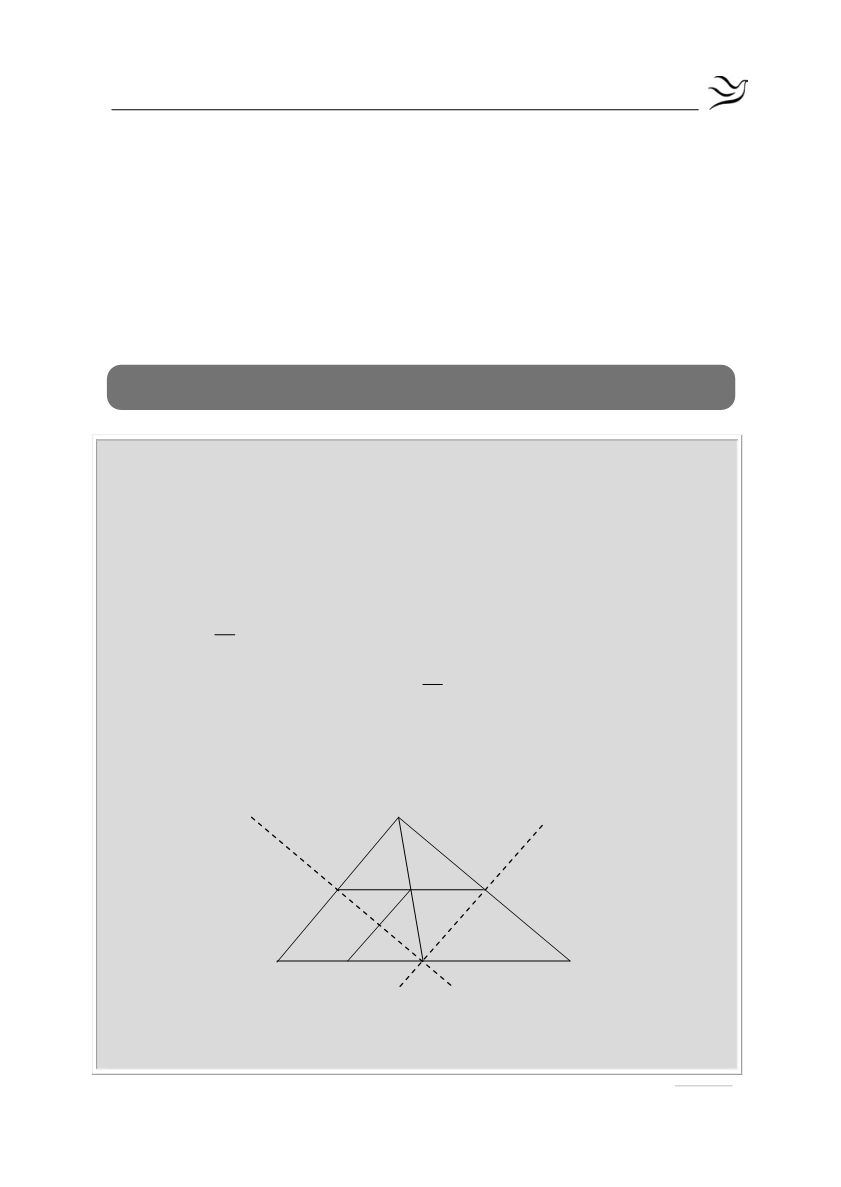
Θεωρούμε τρίγωνο ΑΒΓ και έστω Κ, Λ τα μέσα των ΑΒ, ΑΓ αντίστοιχα.
Φέρουμε τις μεσοκαθέτους μ1, μ2 των πλευρών του ΑΒ και ΑΓ αντίστοιχα, οι
οποίες τέμνονται στο μέσο Μ της ΒΓ.
α) Να αποδείξετε ότι:
i.
το τρίγωνο ΑΒΓ είναι ορθογώνιο με
=
0
Α 90
(Μονάδες 7)
ii.
το τετράπλευρο ΑΛΜΚ είναι ορθογώνιο παραλληλόγραμμο
(Μονάδες 7)
iii.
=
ΒΓ
ΛΘ
4
όπου Θ το σημείο τομής των ΑΜ και ΚΛ. (Μονάδες 6)
β) Αν Ι σημείο της ΒΓ τέτοιο ώστε
=
ΒΓ ΒΙ
4
να αποδείξετε ότι το τετράπλευρο
ΚΘΙΒ είναι παραλληλόγραμμο.
(Μονάδες 7)
Λ
Κ
Β
Α
Γ
Μ
Θ
Ι
μ
1
μ
2
ΘΕΜΑ 4786
205









