Εκδόσεις ΜΠΑΧΑΡΑΚΗ – Τράπεζα Θεμάτων Γεωμετρίας Α’ Γενικού Λυκείου
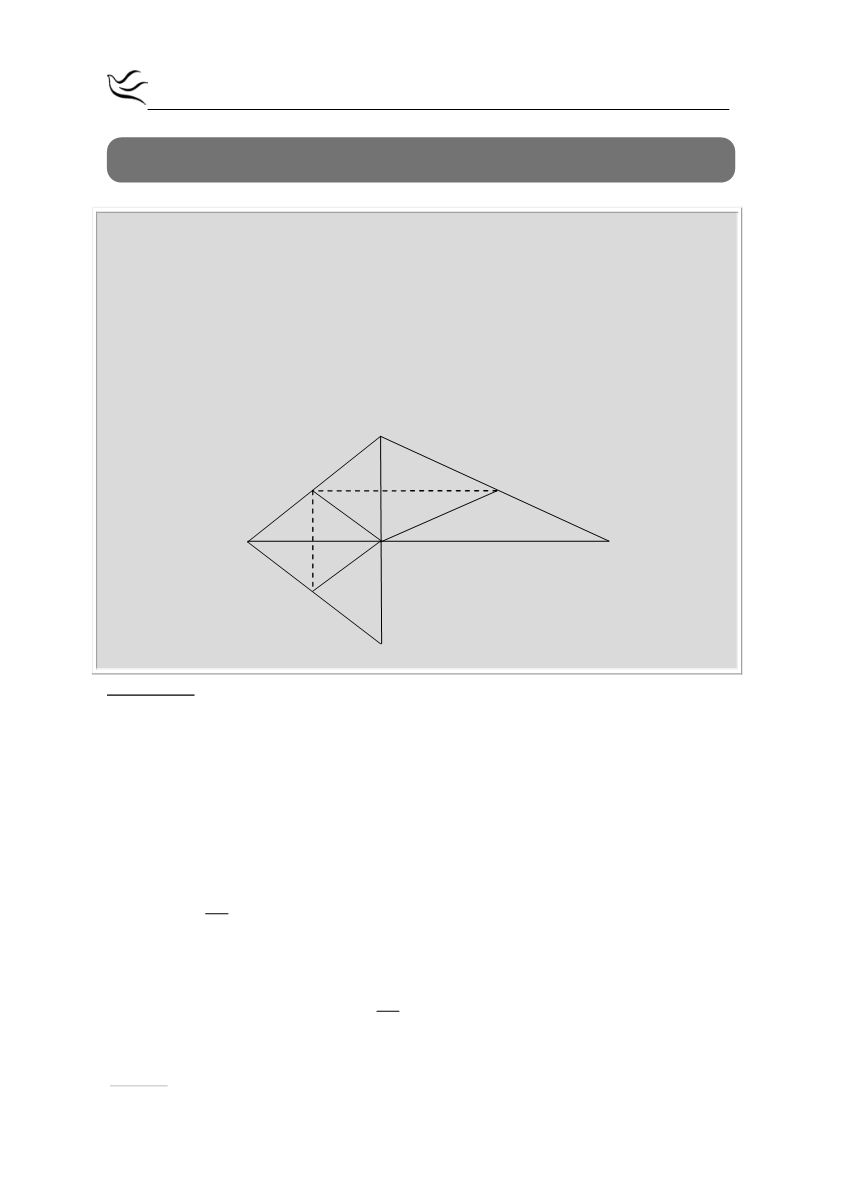
Δίνεται τρίγωνο ΑΒΓ. Στην προέκταση του ύψους του ΑΚ θεωρούμε σημείο Δ
ώστε ΑΚ=ΚΔ. Έστω Λ, Μ, Ν τα μέσα των πλευρών ΑΒ, ΑΓ και ΒΔ αντίστοιχα. Να
αποδείξετε ότι:
α) το τρίγωνο ΑΒΔ είναι ισοσκελές (Μονάδες 7)
β) το τετράπλευρο ΒΛΚΝ είναι ρόμβος (Μονάδες 9)
γ)
⊥
ΛΜ ΛΝ
. (Μονάδες 9)
Απάντηση:
α) Στο τρίγωνο ΑΒΔ to ΒΚ είναι ύψος και διάμεσος άρα, το τρίγωνο ΑΒΔ είναι
ισοσκελές με ΒΑ=ΒΔ.
β) Στο τρίγωνο ΑΒΔ είναι
•
Κ μέσο της ΑΔ
•
Ν μέσο της ΒΔ.
Άρα,
=
ΑΒ
ΚΝ//
2
οπότε και
=
ΚΝ// ΒΛ
δηλαδή το τετράπλευρο ΒΛΚΝ έχει δύο
απέναντι πλευρές του ίσες και παράλληλες συνεπώς, είναι παραλληλόγραμμο.
Ακόμη, στο ορθογώνιο τρίγωνο ΚΒΑ η ΚΛ είναι διάμεσος που αντιστοιχεί στην
υποτείνουσα ΑΒ οπότε είναι
= ⇔ =
ΑΒ ΚΛ
ΚΛ ΛΒ
2
. Δηλαδή το παραλληλόγραμμο
ΒΛΚΝ έχει και δύο διαδοχικές πλευρές του ίσες άρα, είναι ρόμβος.
Δ
Λ
Β
Α
Γ
Μ
Κ
Ν
ΘΕΜΑ 4783
204









