Εκδόσεις ΜΠΑΧΑΡΑΚΗ – Τράπεζα Θεμάτων Γεωμετρίας Α’ Γενικού Λυκείου
άρα και οι χορδές ΒΓ και ΗΖ που περιέχουν τα ίσα τόξα θα είναι παράλληλες
δηλαδή το τετράπλευρο ΒΓΗΖ είναι τραπέζιο.
Τέλος, ισχύει
= ⇔ =
ΒΖ ΓΗ ΒΖ ΓΗ
άρα, το τραπέζιο ΒΓΗΖ είναι ισοσκελές.
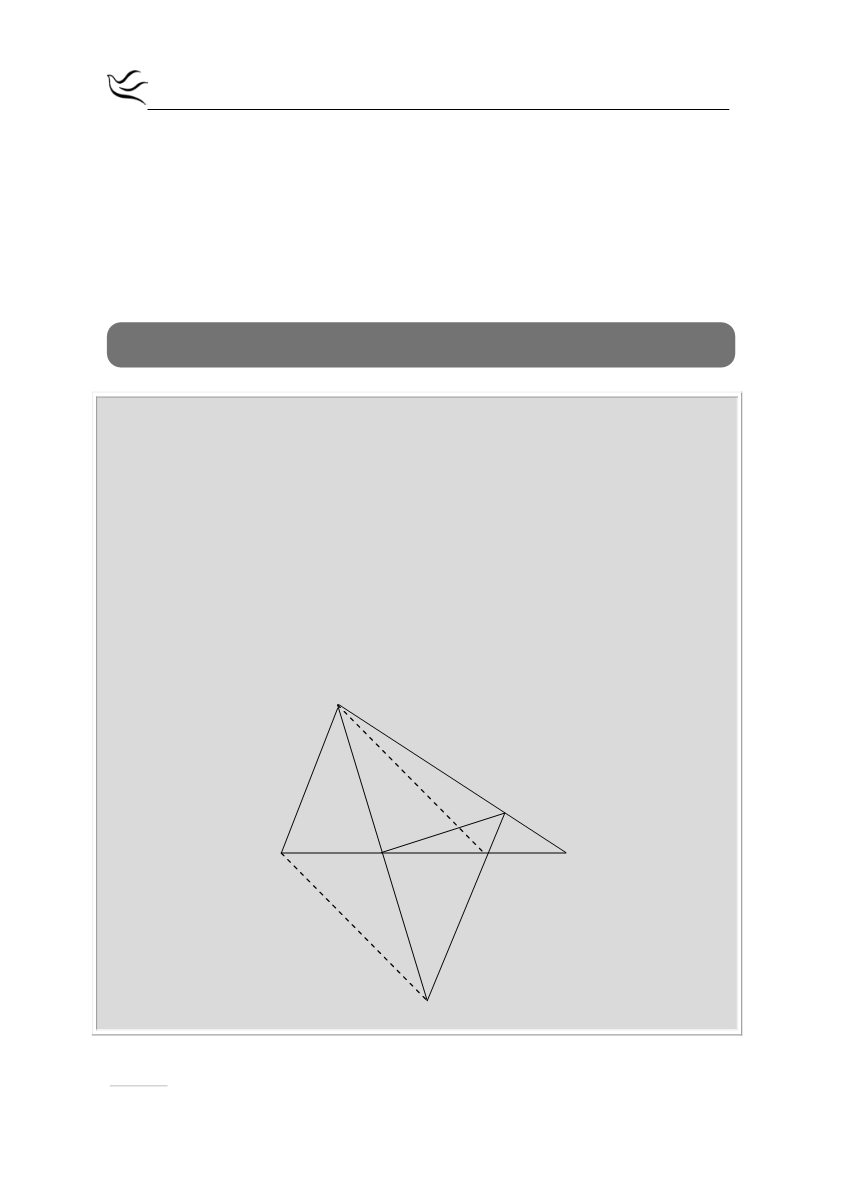
Δίνεται τρίγωνο ΑΒΓ, με ΑΚ διχοτόμο της γωνίας
Α
. Στην προέκταση της ΑΚ
θεωρούμε σημείο Δ ώστε ΑΚ = ΚΔ. Η παράλληλη από το Δ προς την ΑΒ τέμνει
τις ΑΓ και ΒΓ στα Ε και Ζ αντίστοιχα. Να αποδείξετε ότι:
α) το τρίγωνο ΑΕΔ είναι ισοσκελές
(Μονάδες 6)
β) η ΕΚ είναι μεσοκάθετος της ΑΔ
(Μονάδες 6)
γ) τα τρίγωνα ΑΚΒ και ΚΔΖ είναι ίσα
(Μονάδες 7)
δ) το τετράπλευρο ΑΖΔΒ είναι παραλληλόγραμμο.
(Μονάδες 6)
Δ
Ε
Β
Α
Γ
Ζ
Κ
ΘΕΜΑ 4781
202









