Τράπεζα Θεμάτων Γεωμετρίας Α’ Γενικού Λυκείου – Εκδόσεις ΜΠΑΧΑΡΑΚΗ
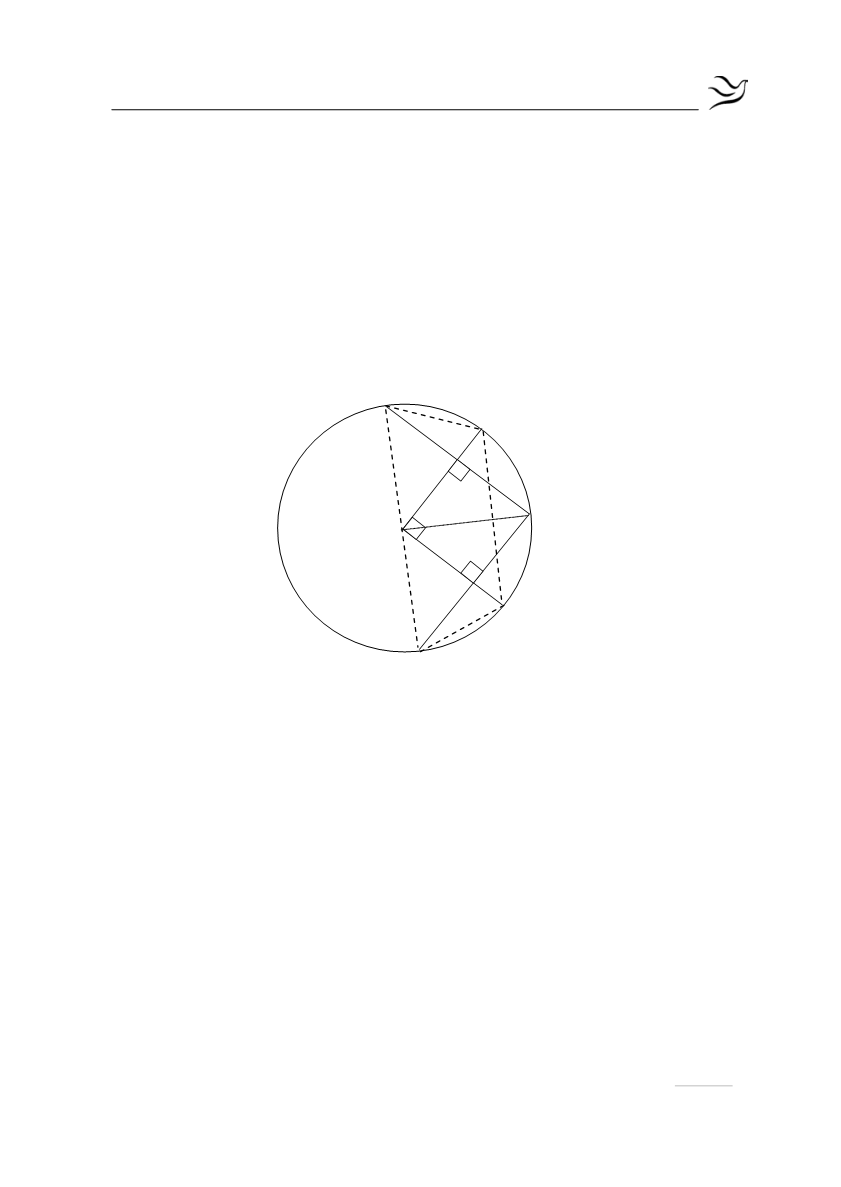
β) το τετράπλευρο ΑΔΟΕ έχει τρεις γωνίες ορθές άρα, είναι ορθογώνιο.
Παρατήρηση:
Επειδή είναι ΟΔ=ΟΕ ως αποστήματα ίσων χορδών το τετράπλευρο ΑΔΟΕ έχει
και δύο διαδοχικές πλευρές ίσες, άρα είναι τετράγωνο.
γ) Για την εγγεγραμμένη γωνία
ΖΑΗ
είναι
=
0
ΖΑΗ 90
. Άρα, η γωνία αυτή βαίνει
σε ημικύκλιο οπότε η ΖΗ είναι διάμετρος του κύκλου. Αυτό σημαίνει ότι τα
σημεία Ζ και Η είναι αντιδιαμετρικά
δ) Στο τρίγωνο ΟΑΖ είναι ΟΖ=ΟΑ ως ακτίνες του κύκλου. Άρα, το τρίγωνο είναι
ισοσκελές με την ΟΔ να είναι το ύψος που αντιστοιχεί στη βάση του ΑΖ. Άρα, η
ΟΔ θα είναι και διχοτόμος οπότε
=
ΖΟΒ ΒΟΑ
(2).
Ομοίως και η ΟΓ είναι διχοτόμος της γωνίας
ΑΟΗ
άρα, θα είναι
=
ΑΟΓ ΗΟΓ
(3)
Από τις σχέσεις (1),(2) και (3) συμπεραίνουμε ότι
= ⇔ =
ΖΟΒ HΟΓ ΒΖ ΓΗ
Δ
Ο
Ε
Η
Α
Γ
Ζ
Β
Μ
201









