Εκδόσεις ΜΠΑΧΑΡΑΚΗ – Τράπεζα Θεμάτων Γεωμετρίας Α’ Γενικού Λυκείου
δηλαδή ότι δύο εντός εναλλάξ γωνίες των ευθειών ΑΓ και ΒΕ που τέμνονται
από την ΑΒ είναι ίσες. Αυτό σημαίνει ότι οι ευθείες ΑΓ και ΒΕ είναι παράλληλες
και ότι το τετράπλευρο ΑΓΒΕ είναι τραπέζιο.
γ) Είναι
= =
0
ΒΓΕ ΓΕΒ 35
άρα, το τρίγωνο ΓΒΕ είναι ισοσκελές.
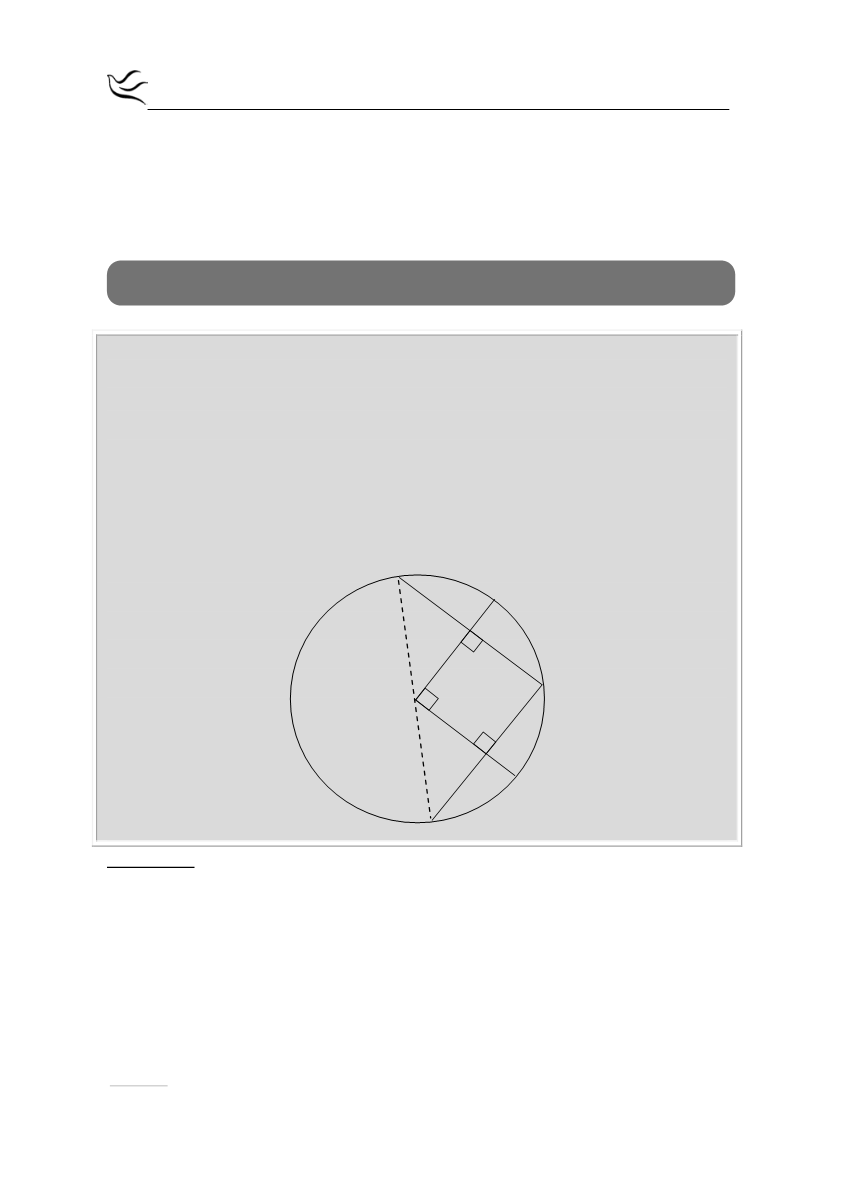
Έστω κύκλος με κέντρο Ο και δύο κάθετες ακτίνες του ΟΒ και ΟΓ. Έστω Α το
μέσον του τόξου
ΒΓ
. Από το Α φέρουμε κάθετες στις ακτίνες ΟΒ και ΟΓ που τις
τέμνουν στα Δ και Ε αντίστοιχα. Οι προεκτάσεις των ΑΔ και ΑΕ τέμνουν τον
κύκλο στα σημεία Ζ και Η αντίστοιχα. Να αποδείξετε ότι:
α) ΑΖ=ΑΗ (Μονάδες 4)
β) το ΑΔΟΕ είναι ορθογώνιο (Μονάδες 7)
γ) τα σημεία Ζ και Η είναι αντιδιαμετρικά (Μονάδες 7)
δ) το τετράπλευρο ΒΓΗΖ είναι ισοσκελές τραπέζιο. (Μονάδες 7)
Απάντηση:
α) Επειδή Α το μέσο του τόξου
ΒΓ
θα είναι
=
ΒΟΑ ΑΟΓ
(1) άρα, η ΟΑ είναι
διχοτόμος της γωνίας
ΒΟΓ
και επειδή Α σημείο της θα ισαπέχει από της
πλευρές της άρα, θα είναι ΑΔ=ΑΕ άρα και 2ΑΔ=2ΑΕ.
Επειδή όμως ΟΔ και ΟΕ τα αποστήματα των χορδών ΑΖ και ΑΗ αντίστοιχα και
τα αποστήματα διέρχονται από τα μέσα των χορδών έχουμε διαδοχικά
ΑΖ=2ΑΔ=2ΑΕ=ΑΗ.
ΘΕΜΑ 4774
Δ
Ο
Ε
Η
Α
Γ
Ζ
Β
200









