Εκδόσεις ΜΠΑΧΑΡΑΚΗ – Τράπεζα Θεμάτων Γεωμετρίας Α’ Γενικού Λυκείου
γ) Αφού ΗΚ//ΜΓ άρα και ΗΚ//ΒΓ. Όμως
⊥
ΒΓ ΑΜ
οπότε και
⊥
ΗΚ ΑΜ
.
Επομένως, προκύπτει ότι στο τρίγωνο ΑΜΖ το σημείο Η θα είναι το ορθόκεντρό
του συνεπώς, θα είναι και
⊥
ΑΗ ΜΖ
(3). Σύμφωνα όμως με το β) ερώτημα είναι
ΜΖ//ΒΔ (4). Από τις σχέσεις (3), (4) συμπεραίνουμε ότι η ευθεία ΑΗ είναι
κάθετη στη ΒΔ.
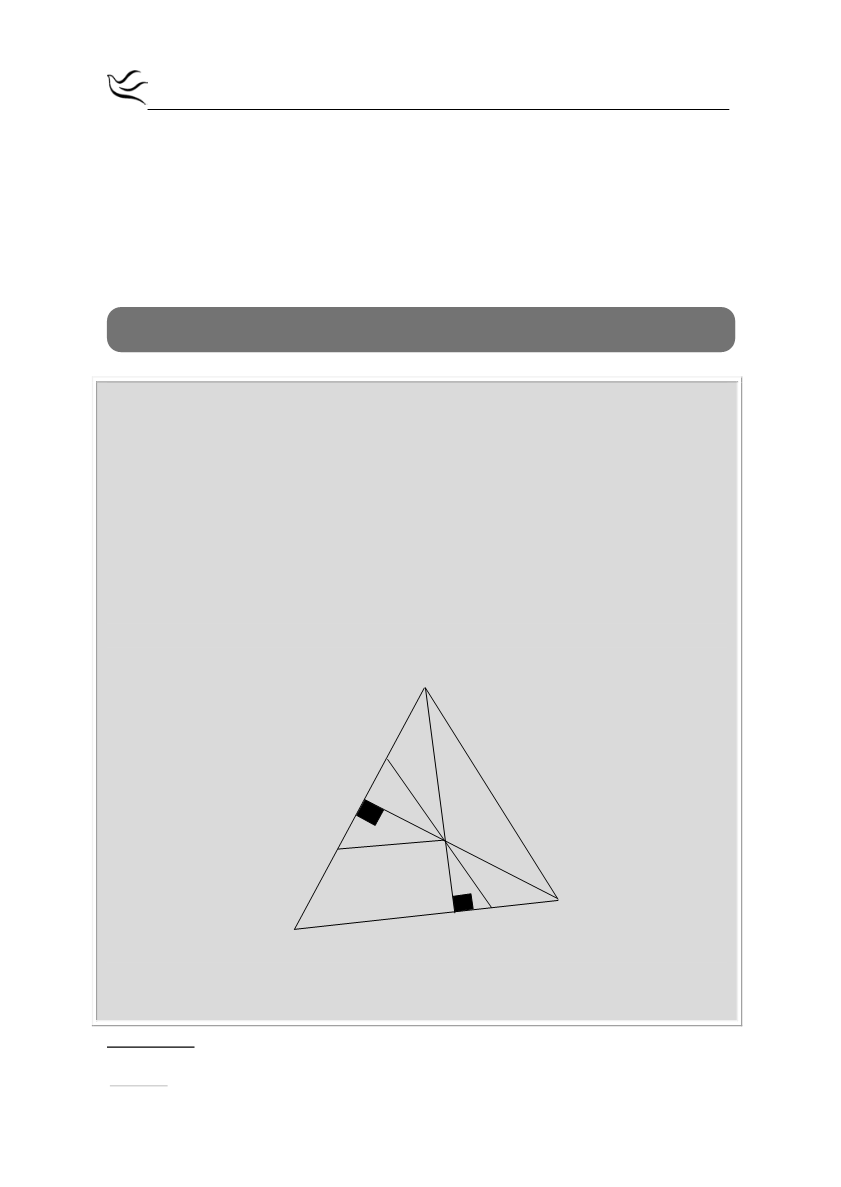
Δίνεται το τρίγωνο ΑΒΓ με γωνία
=
0
Β 60
. Φέρνουμε τα ύψη ΑΔ και ΓΕ που
τέμνονται στο Η. Φέρουμε ΚΖ διχοτόμο της γωνίας
ΕΗΑ
και ΘΗ κάθετο στο
ύψος ΑΔ. Να αποδείξετε ότι:
α) για το τμήμα ΖΕ ισχύει ΖΗ=2ΕΖ
(Μονάδες 9)
β) το τρίγωνο ΘΖΗ είναι ισόπλευρο
(Μονάδες 8)
γ) το τετράπλευρο ΘΗΚΒ είναι ισοσκελές τραπέζιο.
(Μονάδες 8)
Απάντηση:
α) Στο ορθογώνιο τρίγωνο ΑΒΔ είναι
Δ
Β
Γ
Θ
Α
Η
Ε
Ζ
Κ
ΘΕΜΑ 4737
194









