Εκδόσεις ΜΠΑΧΑΡΑΚΗ – Τράπεζα Θεμάτων Γεωμετρίας Α’ Γενικού Λυκείου
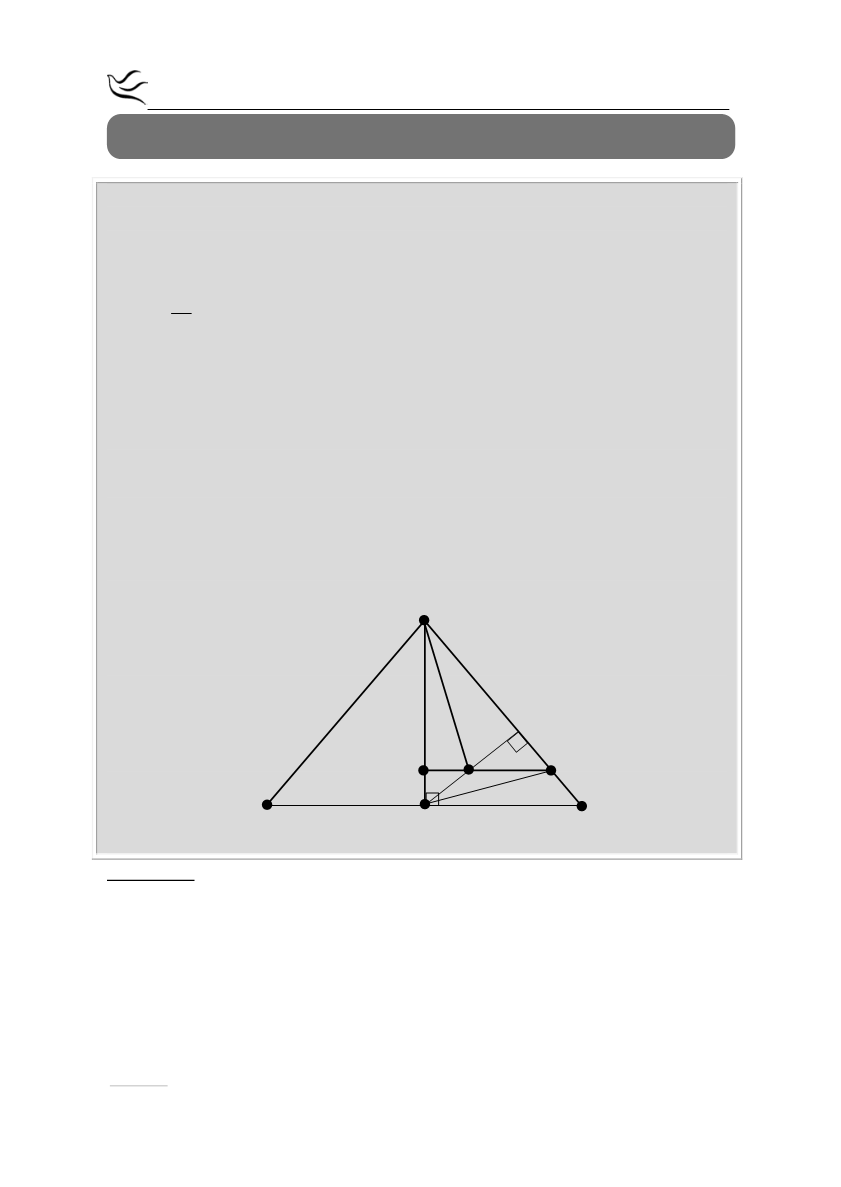
Δίνεται ισοσκελές τρίγωνο ΑΒΓ με ΑΒ = ΑΓ και το ύψος του ΑΜ. Φέρουμε ΜΔ
κάθετη στην ΑΓ και θεωρούμε Η το μέσο του τμήματος ΜΔ. Από το Η φέρουμε
παράλληλη στη ΒΓ η οποία τέμνει τις ΑΜ και ΑΓ στα σημεία Κ και Ζ αντίστοιχα.
Να αποδείξετε ότι:
α)
=
ΒΓ ΗΖ
4
(Μονάδες 9)
β) ΜΖ // ΒΔ
(Μονάδες 8)
γ) η ευθεία ΑΗ είναι κάθετη στη ΒΔ.
(Μονάδες 8)
Απάντηση:
α) Στο τρίγωνο ΔΜΓ είναι
•
Η μέσο της ΔΜ
•
ΗΖ//ΜΓ.
Άρα, Ζ το μέσο της ΔΓ.
Επομένως, στο τρίγωνο ΔΜΓ είναι
ΘΕΜΑ 4731
Α
Β
Δ
Η
Κ
Μ
Γ
Ζ
192









