Τράπεζα Θεμάτων Γεωμετρίας Α’ Γενικού Λυκείου – Εκδόσεις ΜΠΑΧΑΡΑΚΗ
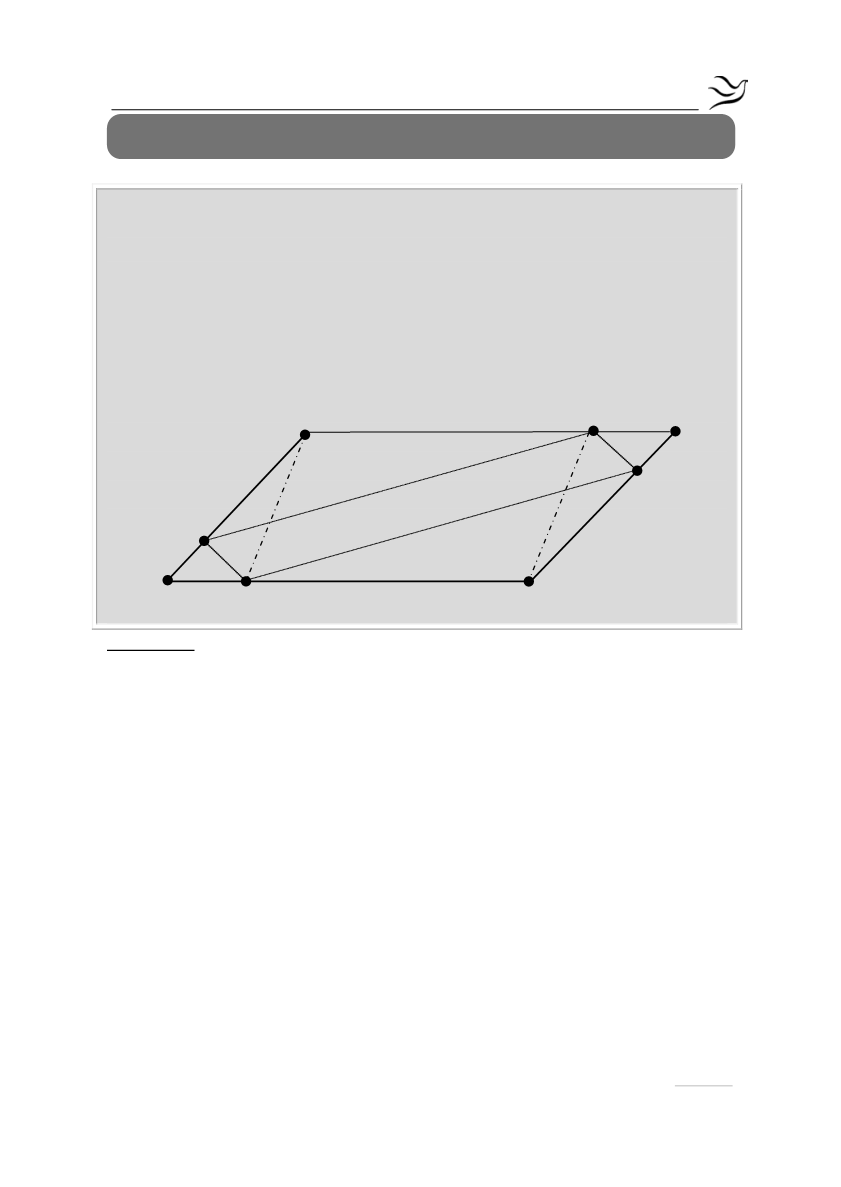
Σε παραλληλόγραμμο ΑΒΓΔ θεωρούμε σημεία Ε, Ζ, Η, Θ στις πλευρές ΑΒ, ΒΓ,
ΓΔ, ΔΑ αντίστοιχα, με ΑΕ=ΓΗ και ΒΖ=ΔΘ. Να αποδείξετε ότι:
α) το τετράπλευρο ΑΕΓΗ είναι παραλληλόγραμμο
(Μονάδες 6)
β) το τετράπλευρο ΕΖΗΘ είναι παραλληλόγραμμο
(Μονάδες 10)
γ) τα τμήματα ΑΓ, ΒΔ, ΕΗ και ΖΘ διέρχονται από το ίδιο σημείο.
(Μονάδες 9)
Απάντηση:
α) Σύμφωνα με τα δεδομένα είναι
ΑΕ//=ΓΗ
άρα, το τετράπλευρο ΑΕΓΗ έχει δύο απέναντι πλευρές του ίσες και παράλληλες
άρα, είναι παραλληλόγραμμο.
β) Τα τρίγωνα ΑΘΕ και ΓΖΗ είναι ίσα γιατί
•
ΑΕ=ΓΗ
•
= − = − =
ΑΘ ΑΔ ΘΔ ΒΓ ΒΖ ΖΓ
•
=
Α Γ
ως απέναντι γωνίες παραλληλογράμμου.
Άρα και
ΘΕ=ΗΖ (1).
ΘΕΜΑ 4651
Α
Β
Δ
Ε
Θ
Η
Ζ
Γ
187









