Εκδόσεις ΜΠΑΧΑΡΑΚΗ – Τράπεζα Θεμάτων Γεωμετρίας Α’ Γενικού Λυκείου
Άρα και
=
ΔΑΡ ΔΒΡ
.
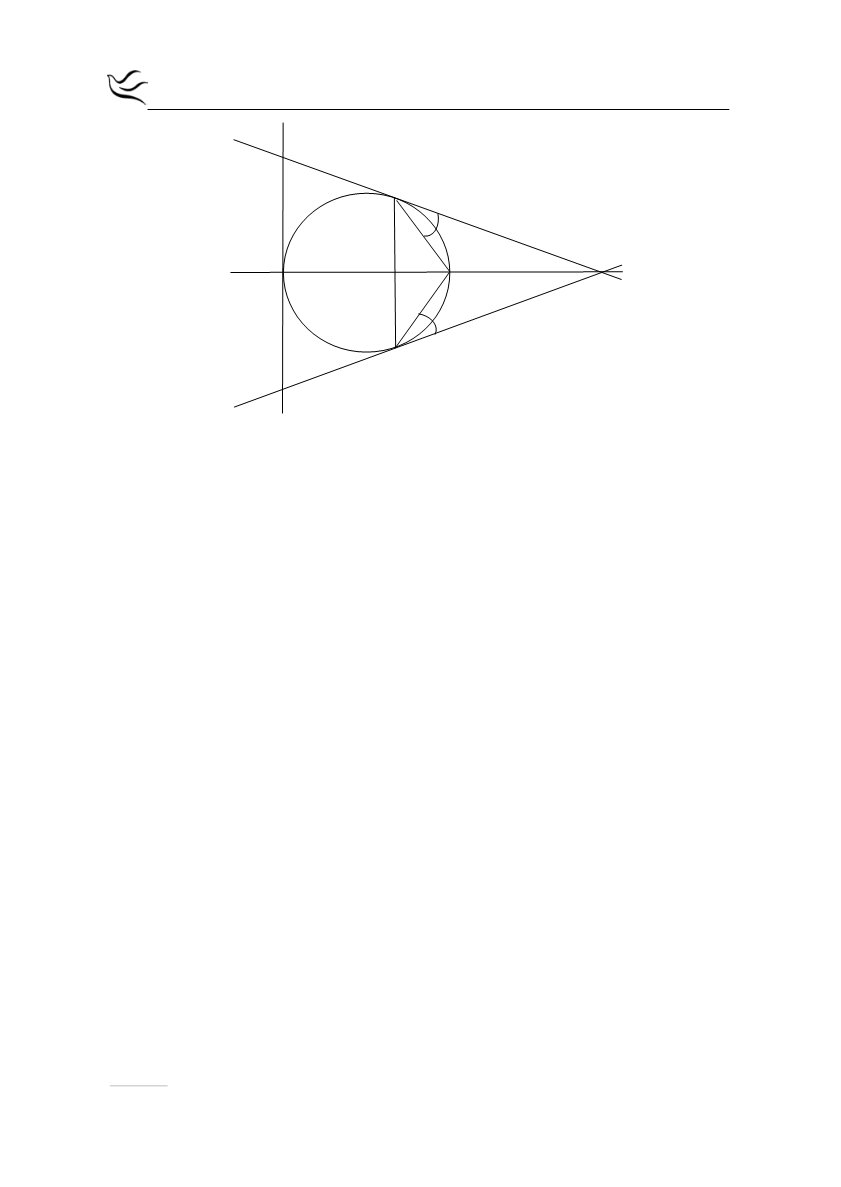
β) Η εφαπτομένη του κύκλου στο σημείο Γ είναι κάθετη στην ακτίνα ΟΓ άρα και
στη διακεντρική ευθεία οπότε σύμφωνα και με το α) ερώτημα στο τρίγωνο ΡΕΖ
η ΡΓ είναι διχοτόμος και ύψος άρα, το τρίγωνο ΡΕΖ είναι ισοσκελές με
ΡΕ=ΡΖ (1).
Επίσης, είναι
ΡΑ=ΡΒ (2).
Από τις σχέσεις (1) και (2) με αφαίρεση κατά μέλη προκύπτει
− = − ⇔ =
ΡΕ ΡΑ ΡΖ ΡΒ ΕΑ ΖΒ
.
γ) Η διακεντρική ευθεία είναι μεσοκάθετη της χορδής ΑΒ επομένως, είναι
⊥
ΡΟ ΑΒ
(3).
Ακόμη, στο β) ερώτημα έχουμε αποδείξει ότι
⊥
ΡΟ ΕΖ
(4).
Από τις σχέσεις (3) και (4) συμπεραίνουμε ότι ΑΒ//ΕΖ άρα, το τετράπλευρο
ΑΒΖΕ είναι τραπέζιο.
Επειδή όμως στο β) ερώτημα έχουμε αποδείξει ότι ΕΑ=ΖΒ το τραπέζιο ΑΒΖΕ
είναι και ισοσκελές.
B
A
●
Δ
Ο
Ρ
●
●
●
●
●
●
Ζ
Ε
Γ ●
184









