Εκδόσεις ΜΠΑΧΑΡΑΚΗ – Τράπεζα Θεμάτων Γεωμετρίας Α’ Γενικού Λυκείου
Δίνεται ορθογώνιο τρίγωνο
ΑΒΓ
(
=
0
Α 90
) και
=
0
Γ 30
με Μ και Ν τα μέσα των
πλευρών ΒΓ και ΑΒ αντίστοιχα. Έστω ότι η μεσοκάθετος της πλευράς ΒΓ τέμνει
την ΑΓ στο σημείο Ε.
α) Να αποδείξετε ότι:
i) η ΒΕ είναι διχοτόμος της γωνίας
Β
(Μονάδες 6)
ii)
=
ΓΕ ΑΕ
2
(Μονάδες 6)
iii) η ΒΕ είναι μεσοκάθετος της διαμέσου ΑΜ. (Μονάδες 7)
β) Αν ΑΔ είναι το ύψος του τριγώνου
ΑΒΓ
που τέμνει την ΒΕ στο Η, να
αποδείξετε ότι τα σημεία Μ, Η και Ν είναι συνευθειακά.
(Μονάδες 6)
Απάντηση:
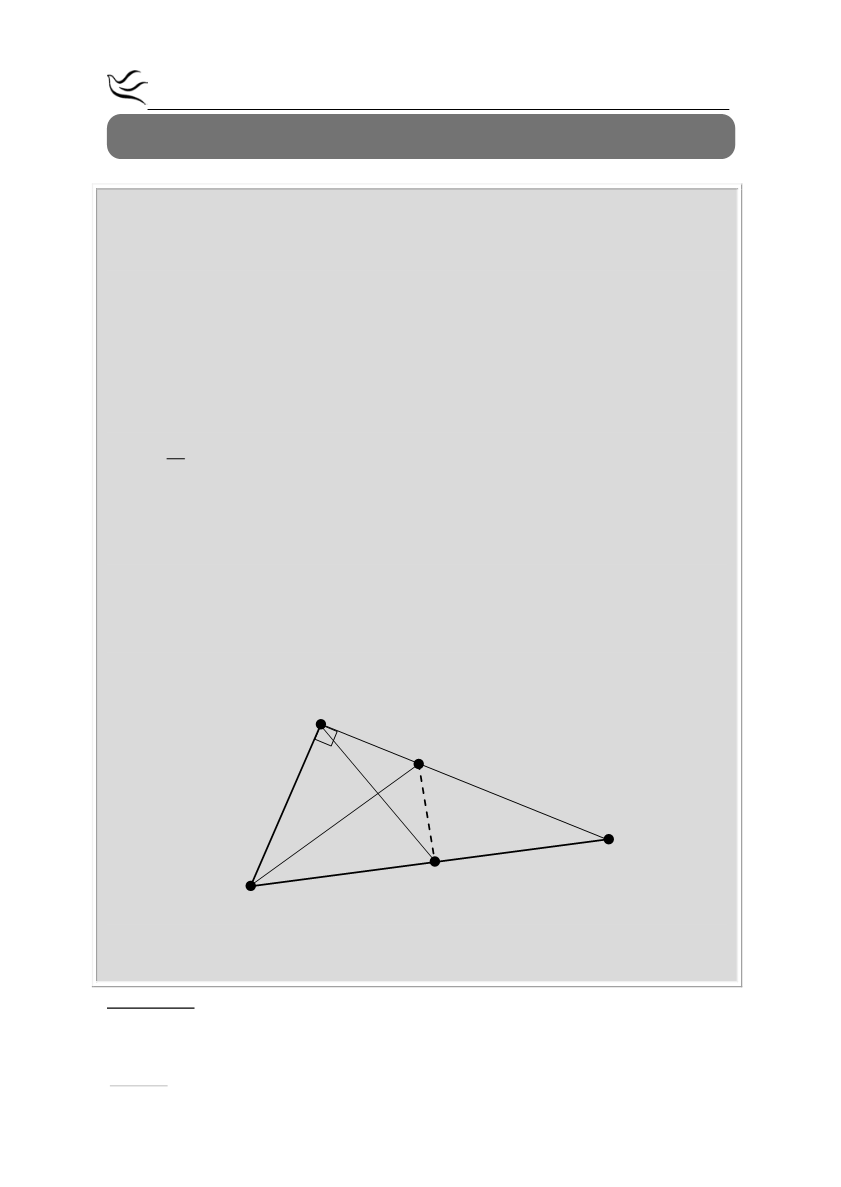
α) i) Στο ορθογώνιο τρίγωνο ΑΒΓ η ΑΜ είναι η διάμεσος που αντιστοιχεί στην
υποτείνουσα ΒΓ.
Α
Ν
Μ
Β
Ε
Γ
●
ΘΕΜΑ 4646
180









