Εκδόσεις ΜΠΑΧΑΡΑΚΗ – Τράπεζα Θεμάτων Γεωμετρίας Α’ Γενικού Λυκείου
Δίνεται ορθογώνιο τρίγωνο ΑΒΓ (
=
0
Α 90
). Φέρουμε τη διάμεσο του ΑΜ την
οποία προεκτείνουμε (προς το μέρος του Μ) κατά τμήμα ΜΔ = ΑΜ. Θεωρούμε
ευθεία ΔΚ κάθετη στη ΒΓ, η οποία τέμνει τη διχοτόμο της γωνίας
Β
στο Ε. Να
αποδείξετε ότι:
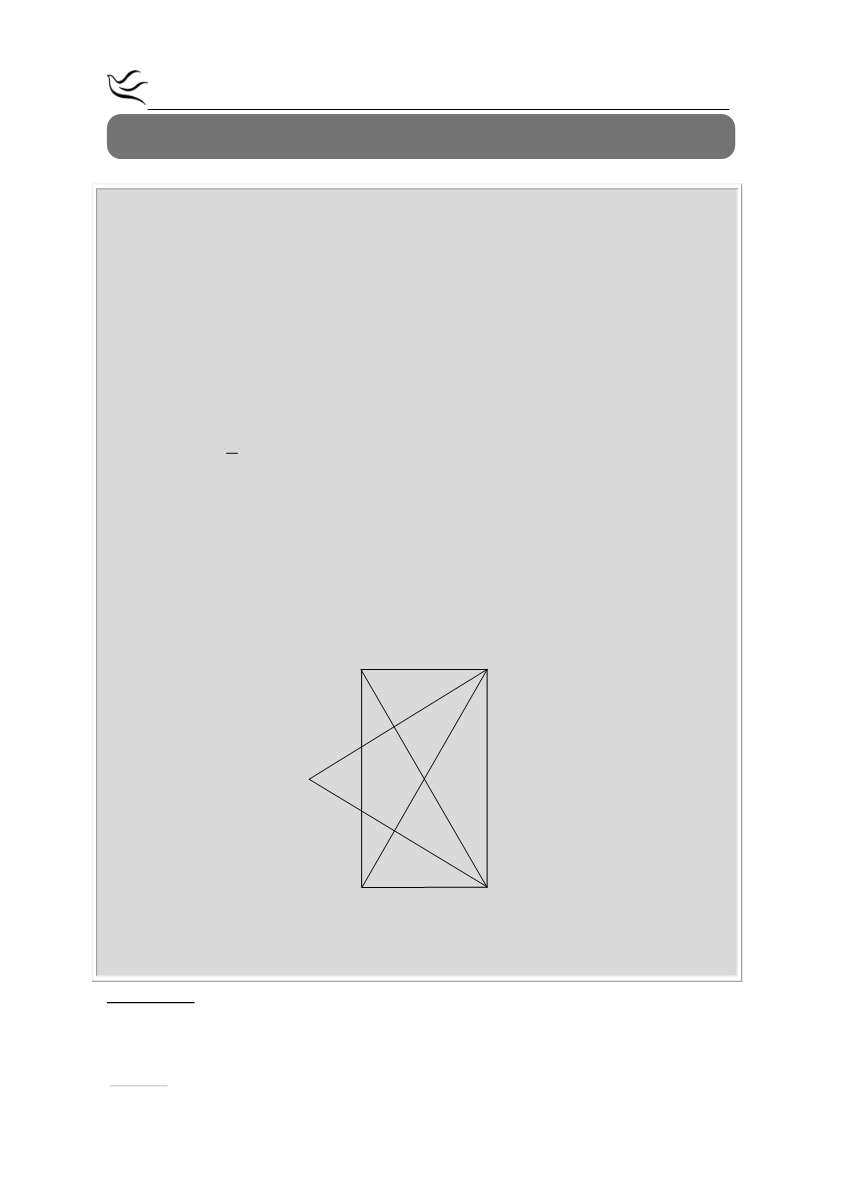
α) το τετράπλευρο ΑΒΔΓ είναι ορθογώνιο
(Μονάδες 8)
β)
= −
0
Β
ΚΕΒ 90
2
(Μονάδες 8)
γ) ΔΕ=ΒΔ.
(Μονάδες 9)
Απάντηση:
α) Επειδή ΑΜ διάμεσος του τριγώνου ΑΒΓ είναι
ΓΜ=ΜΒ.
Α
Β
Δ
Ε
Γ
Μ
Κ
ΘΕΜΑ 4643
178









