Τράπεζα Θεμάτων Γεωμετρίας Α’ Γενικού Λυκείου – Εκδόσεις ΜΠΑΧΑΡΑΚΗ
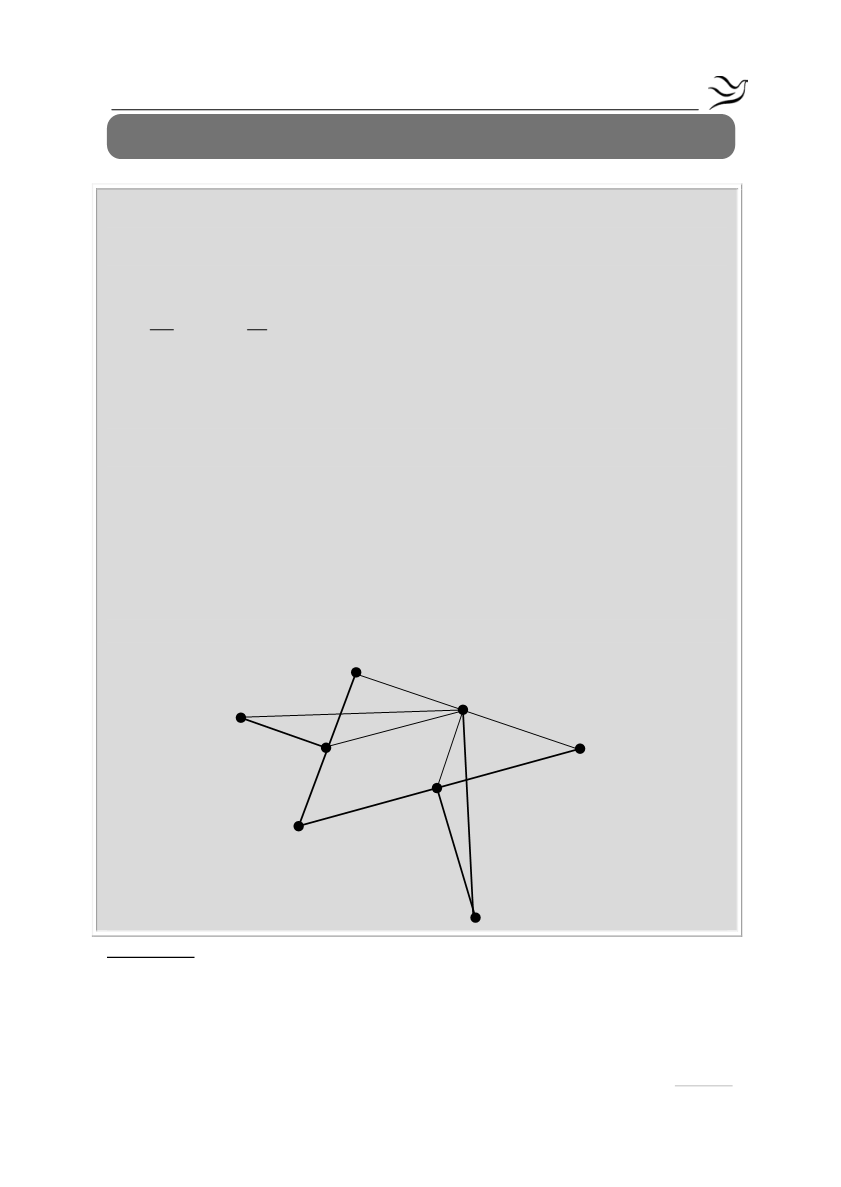
Δίνεται τρίγωνο ΑΒΓ με γωνίες Β και Γ οξείες και Δ, Μ και Ε τα μέσα των
πλευρών του ΑΒ, ΑΓ και ΒΓ αντίστοιχα. Στις μεσοκάθετες των ΑΒ και ΒΓ και
εκτός του τριγώνου ΑΒΓ θεωρούμε σημεία Ζ και Η αντίστοιχα, τέτοια ώστε
=
ΑΒ ΔΖ
2
και
=
ΒΓ ΕΗ
2
.
α) Να αποδείξετε ότι:
ί. το τετράπλευρο ΒΔΜΕ είναι παραλληλόγραμμο
(Μονάδες 5)
ίί. τα τρίγωνα ΖΔΜ και ΕΜΗ είναι ίσα.
(Μονάδες 10)
β) Αν τα σημεία Ζ, Δ, Ε είναι συνευθειακά, να αποδείξετε ότι η
=
0
Α 90
.
(Μονάδες 10)
Απάντηση:
α) ί. Στο τρίγωνο ΑΒΓ είναι
•
Δ μέσο της ΑΒ
•
Μ μέσο της ΑΓ.
Γ
Β
Μ
Ε
Ζ
Δ
Η
Α
ΘΕΜΑ 4640
175









