Εκδόσεις ΜΠΑΧΑΡΑΚΗ – Τράπεζα Θεμάτων Γεωμετρίας Α’ Γενικού Λυκείου
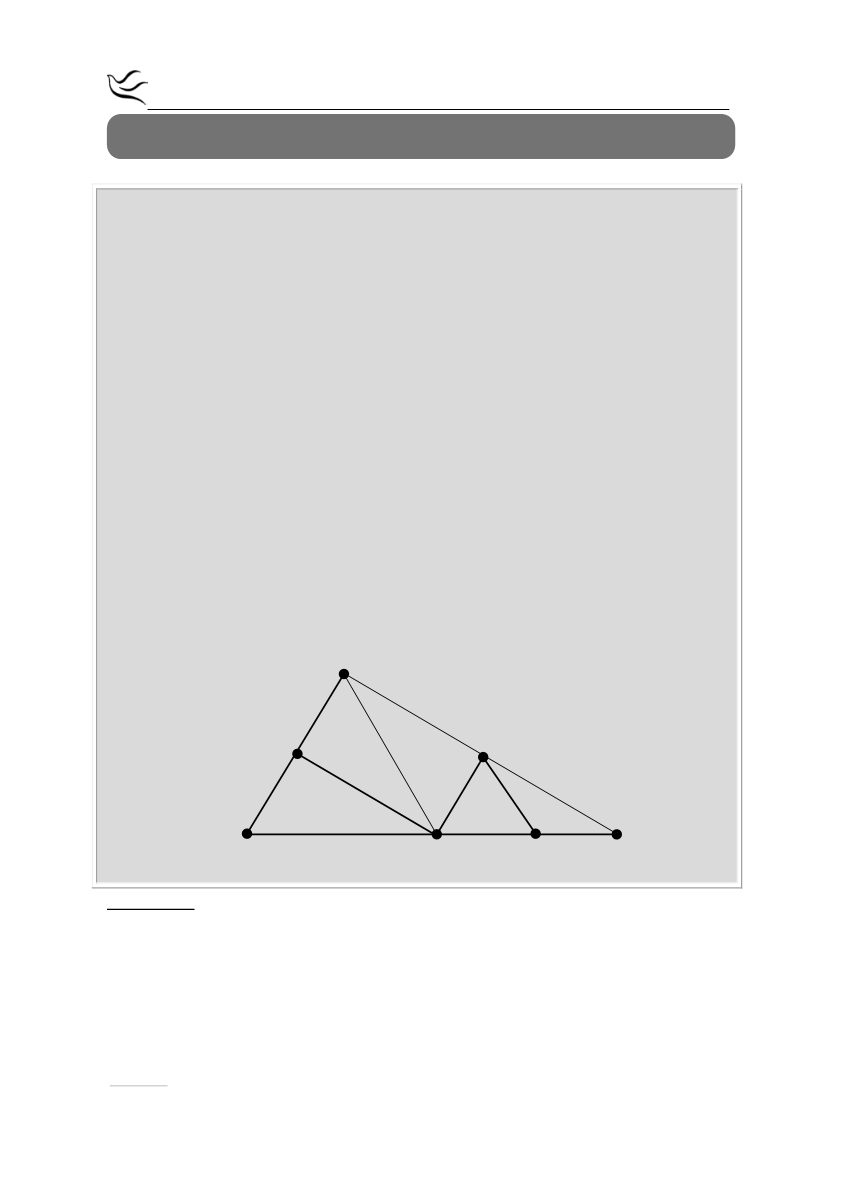
Σε μια ευθεία (ε) θεωρούμε διαδοχικά τα σημεία Α, Β, Γ έτσι ώστε ΑΒ = 2ΒΓ και
στο ίδιο ημιεπίπεδο θεωρούμε ισόπλευρα τρίγωνα ΑΒΔ και ΒΓΕ. Αν Η είναι το
μέσο του ΑΔ και η ευθεία ΔΕ τέμνει την ευθεία (ε) στο σημείο Ζ να αποδείξετε
ότι:
α) το τετράπλευρο ΒΗΔΕ είναι ορθογώνιο
(Μονάδες 8)
β) το τρίγωνο ΓΖΕ είναι ισοσκελές
(Μονάδες 8)
γ) το τετράπλευρο ΗΕΓΑ είναι ισοσκελές τραπέζιο.
(Μονάδες 9)
Απάντηση:
α) Επειδή τα τρίγωνα ΑΒΔ και ΒΓΕ είναι ισόπλευρα είναι
= = =
0
ΑΒΔ ΒΔΑ ΕΒΓ 60
(1).
Όμως
+ + = ⇔
(1)
0
ΑΒΔ ΔΒΕ ΕΒΓ 180
+ + = ⇔
0
0
0
60 ΔΒΕ 60 180
= − ⇔
0
0
ΔΒΕ 180 120
ΘΕΜΑ 4626
Α
Δ
Η
Ε
Ζ
Γ
Β
172









