Εκδόσεις ΜΠΑΧΑΡΑΚΗ – Τράπεζα Θεμάτων Γεωμετρίας Α’ Γενικού Λυκείου
Από τις σχέσεις (3) και (4) συμπεραίνουμε ότι
=
ΓΕΖ Ζ
δηλαδή ότι το τρίγωνο ΓΖΕ είναι ισοσκελές με
ΓΕ=ΓΖ (5).
γ) Ισχύει διαδοχικά ότι
= + = + = + = = =
(5)
ΒΖ ΒΓ ΓΖ ΒΓ ΓΕ ΒΓ ΒΓ 2ΒΓ ΑΒ ΒΔ
.
Επομένως, το τρίγωνο ΒΔΖ είναι ισοσκελές και το ΒΕ είναι ύψος που αντιστοιχεί
στη βάση ΔΖ άρα, είναι και διάμεσος. Συνεπώς, το Ε είναι μέσο της ΔΖ.
Έτσι στο τρίγωνο ΔΑΖ είναι
•
Η μέσο της ΔΑ
•
Ε μέσο της ΔΖ.
Άρα, ΗΕ//ΑΓ οπότε το τετράπλευρο ΗΕΓΑ είναι τραπέζιο.
Τέλος, ισχύει
= =
0
Α Γ 60
Άρα, το τραπέζιο έχει τις δύο προσκείμενες στη βάση του ΑΓ γωνίες ίσες άρα,
θα είναι και ισοσκελές.
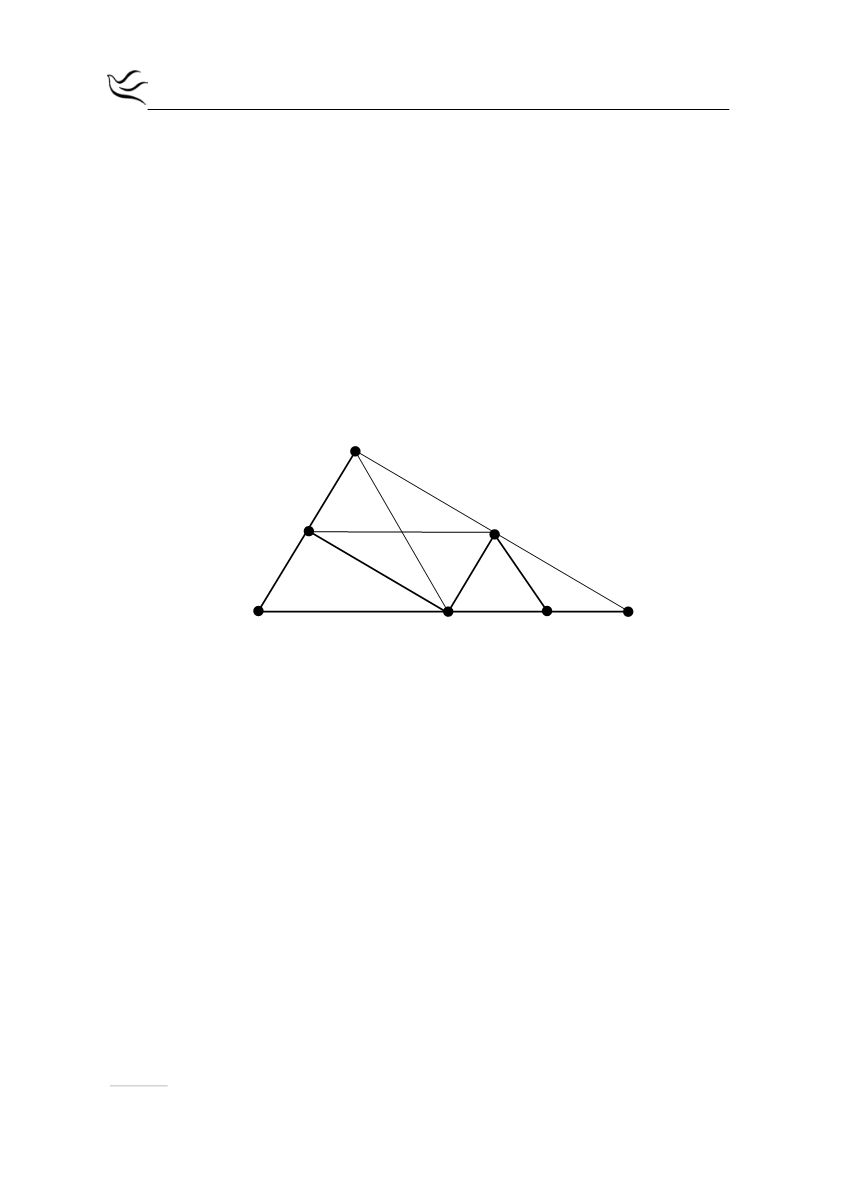
Α
Δ
Η
Ε
Ζ
Γ
Β
174









