Εκδόσεις ΜΠΑΧΑΡΑΚΗ – Τράπεζα Θεμάτων Γεωμετρίας Α’ Γενικού Λυκείου
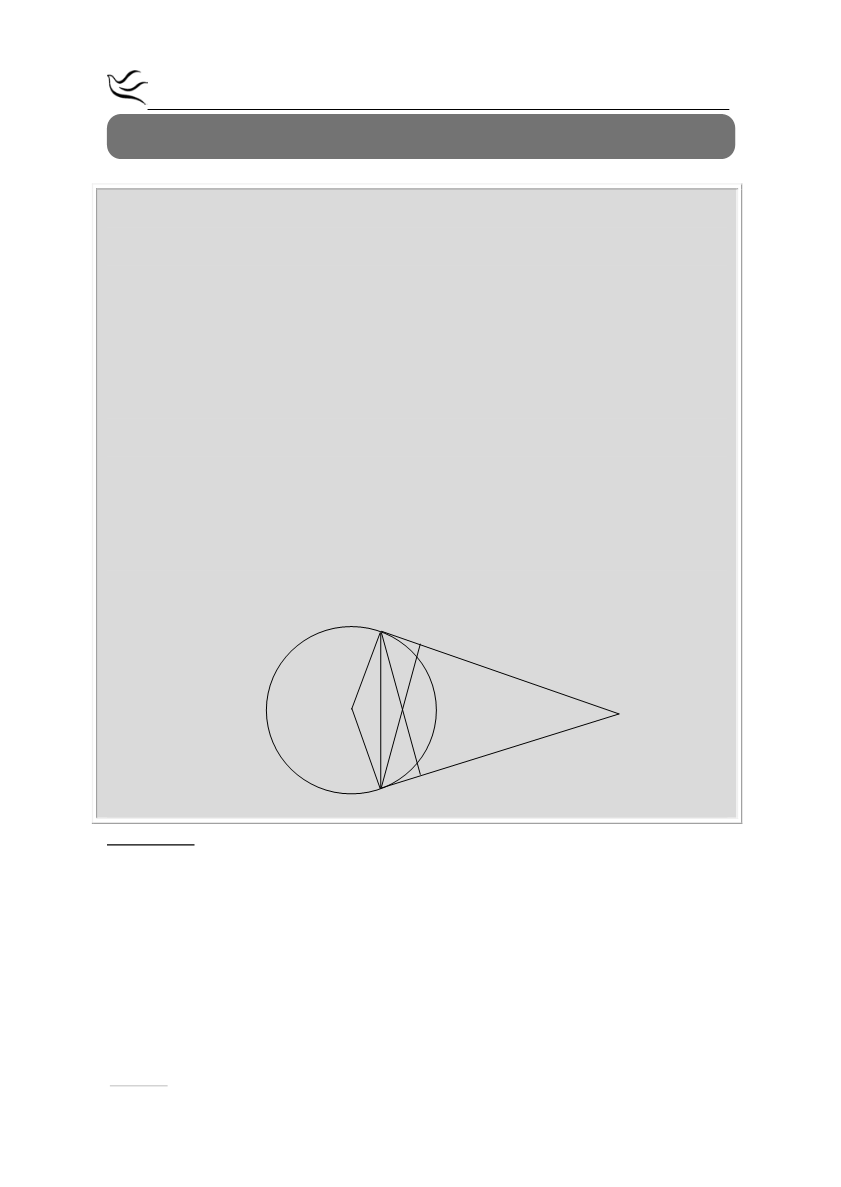
Δίνεται κύκλος κέντρου Ο και δυο μη αντιδιαμετρικά σημεία του Α και Β.
Φέρουμε τις εφαπτόμενες του κύκλου στα σημεία Α και Β οι οποίες τέμνονται
στο σημείο Γ. Φέρουμε επίσης και τα ύψη ΑΔ και ΒΕ του τριγώνου ΑΒΓ τα
οποία τέμνονται στο σημείο Η. Να αποδείξετε ότι:
α) το τρίγωνο ΒΗΑ είναι ισοσκελές
(Μονάδες 8)
β) το τετράπλευρο ΟΒΗΑ είναι ρόμβος
(Μονάδες 9)
γ) τα σημεία Ο, Η, Γ είναι συνευθειακά.
(Μονάδες 8)
Απάντηση:
α) Είναι ΓΑ=ΓΒ ως τα εφαπτόμενα τμήματα άρα το τρίγωνο ΓΑΒ είναι ισοσκελές
με
=
ΓΒΑ ΓΑΒ
.
Τα τρίγωνα ΑΒΕ και ΑΒΔ είναι ίσα γιατί
•
= =
0
ΒΕΑ ΑΔΒ 90
•
ΑΒ κοινή
•
=
ΒΑΕ ΑΒΔ
αφού
=
ΓΑΒ ΓΒΑ
.
Α
Β
Γ
Η
Ε
Δ
Ο
ΘΕΜΑ 4606
170









