Τράπεζα Θεμάτων Γεωμετρίας Α’ Γενικού Λυκείου – Εκδόσεις ΜΠΑΧΑΡΑΚΗ
β) Έστω ότι οι διαγώνιοι του ορθογωνίου ΑΖΒΗ τέμνονται στο Κ. Επειδή είναι
ίσες και διχοτομούνται είναι
= = =
ΑΒ ΗΖ
ΚΑ
ΚΖ
2 2
άρα, το τρίγωνο ΚΑΖ είναι ισοσκελές με
= ⇔ =
ΚZΑ ΚΑΖ ΗZΑ ΖAΓ
.
γ) Επειδή οι εντός εναλλάξ γωνίες
ΗZΑ
και
ΖAΓ
των ευθειών ΗΖ και ΑΓ, που
τέμνονται από την ΑΖ, είναι ίσες θα είναι ΗΖ//ΑΓ.
Έτσι, στο τρίγωνο ΑΒΓ είναι
•
Κ μέσο της ΑΒ
•
ΚΖ//ΑΓ.
Άρα, η ευθεία ΗΖ διέρχεται από το Μ.
δ) Στο τρίγωνο ΑΒΓ είναι
•
Μ μέσο της ΒΓ
•
Κ μέσο της ΑΒ.
Άρα,
=
ΑΓ
ΜΚ //
2
οπότε έχουμε διαδοχικά
+
= + = + = + =
ΑΓ ΗΖ ΑΓ ΑΒ ΑΓ ΑΒ
ΜΗ ΜΚ ΚΗ
2 2 2 2
2
.
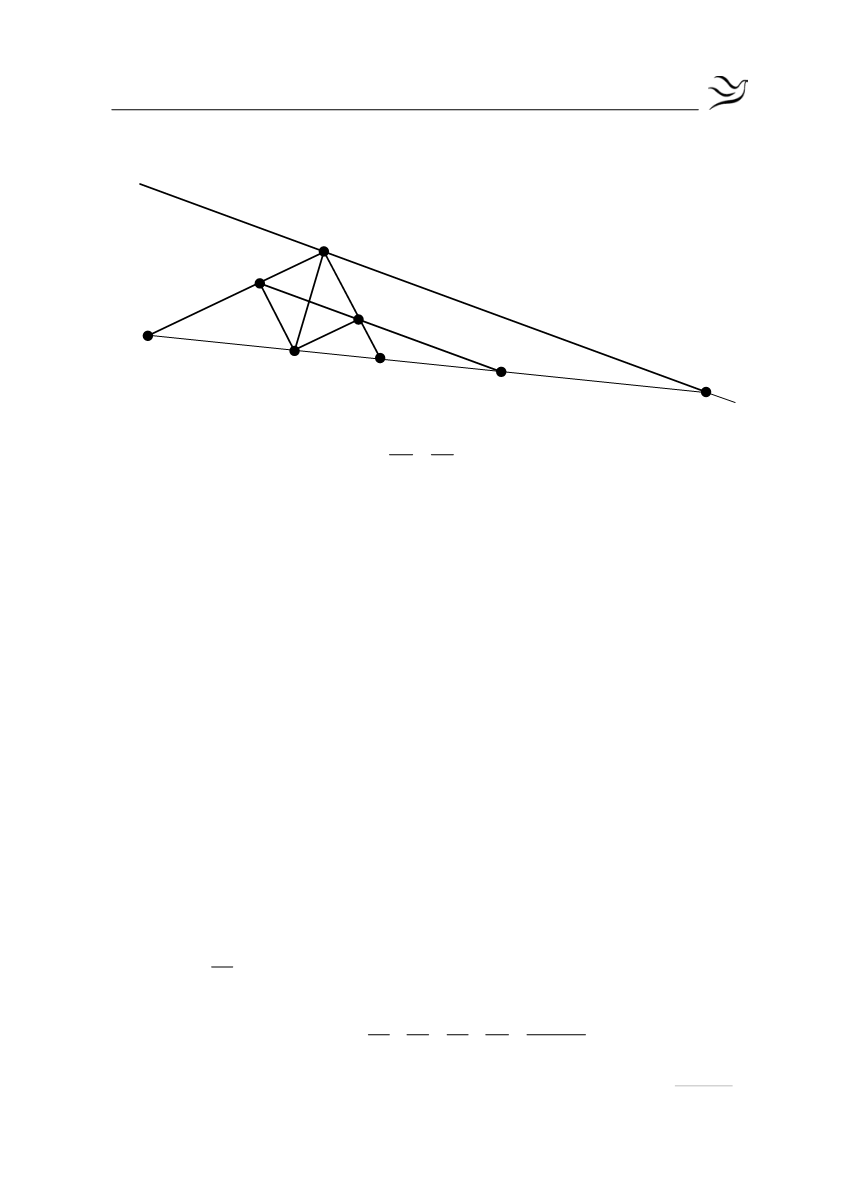
Κ
Μ
Ζ
Β
Ε
Η
Δ
Α
●
Γ
165









